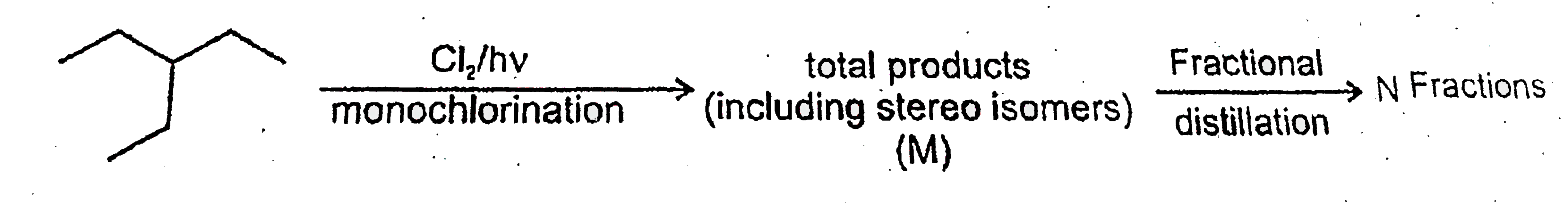
The value of M and N are respectively.
3.2
3,3
4,3
3,4
The correct Answer is:3

Total isomers =4, Fractions =3
Topper's Solved these Questions
- BOOK - RESONANCECHAPTER - TEST PAPERSEXERCISE - FST test -230videos
TEST PAPERS
- BOOK - RESONANCECHAPTER - TEST PAPERSEXERCISE - FST-330videos
TEST PAPERS
- BOOK - RESONANCECHAPTER - TEST PAPERSEXERCISE - PT-0630videos
TEST PAPERS
- BOOK - RESONANCECHAPTER - SIMPLE HARMONIC MOTION EXERCISE - Advanced Level Problems13videos
SIMPLE HARMONIC MOTION
- BOOK - RESONANCECHAPTER - TEST SERIESEXERCISE - PHYSICS127videos
TEST SERIES
Similar Questions
Knowledge Check
- Question 1 - Select One
Two finite sets have m and n elements. The number of subsets of the first set is 112 more than that of the second set. The values of m and n are, respectively.
A4,7B7,4C4,4D7,7 - Question 2 - Select One
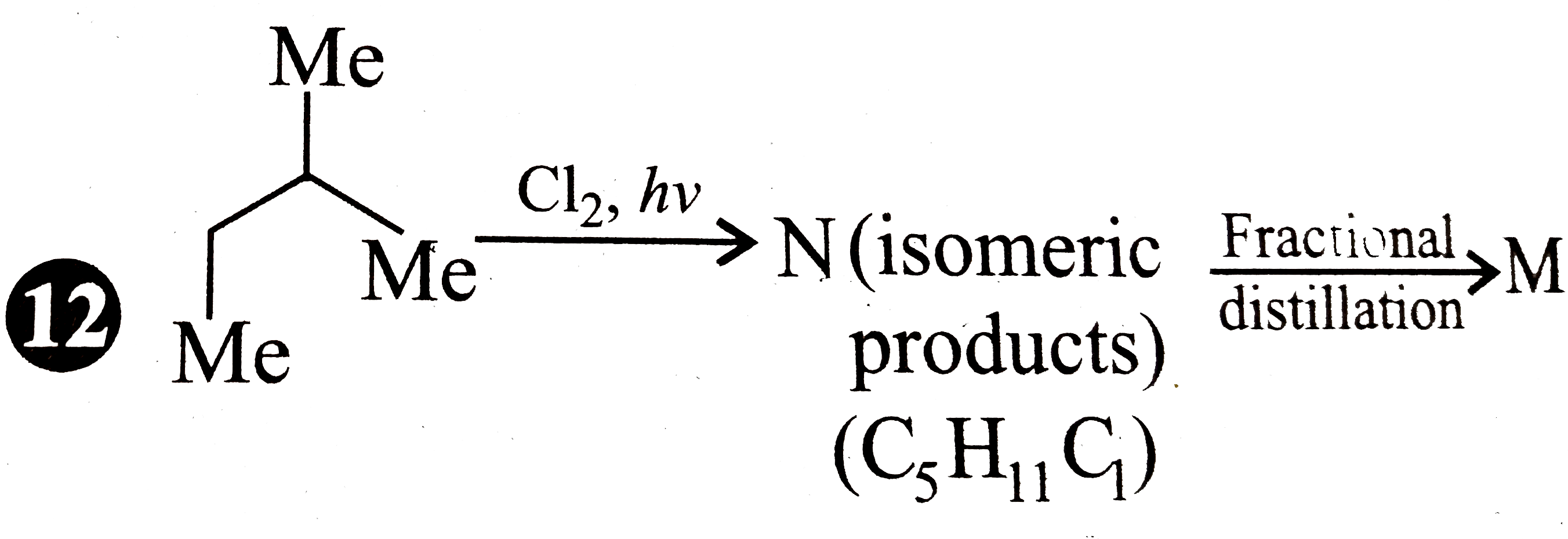
The value of N and M are:A(a) 3,3B(b) 4,4C(c) 6,6D(d) 6,4 - Question 3 - Select One
Two finite sets have m and n elements, respectively. The total number of subsets of first set is 56 more than the total number of subsets of the second set. The value of m and n respectively are
A7, 6B5, 1C6, 3D8, 7
What are the values of MandN respectively if M39048458N is divisible by both 8 and 11, where MandN are single-digit integers?
View SolutionSolve for X, if IX S 1. Two finite sets have m and n elements. The total number of subsets of the first set is 56 more than the total number of subsets of the second set. Find the value of m and n. respectively. can be the (f A and B be two sets containing 3 and 6 elements What
View SolutionA number when divided by 7 leaves a remainder 3 and the resulting quotient when divided by 11 leaves a remainder 6. If the same number when divided by 11 leaves a remainder m and the resulting quotient when divided by 7 leaves a remainder n. What are the values of m and n respectively ?
View SolutionTwo finite sets have m and n elements. The number of subsets of the first set is 112 more than that of the second set. The values of m and n are, respectively.
View SolutionIf A(2,3,−4),B(m,1,−1),C(3,2,2)andG(3,2,n) is the centroid of ΔABC, then the values of m and n respectively are
View Solution

