Line OQ is angle bisector of angle O of right angle triangle OPR, right angle at P. Point Q is such that ORQP is concyclic. If point O is orign and points P,Q,R are represented by the complex numbers z3,z2,z1 respectively. If z22z1z2=32 then (R is circum radius of △OPR)
Angles of △OPR are π6,π3,π2
Angles of △OPR are π4,π4,π2
Area of △OPR is 2√2R2
Area of △OPR is 2R2
The correct Answer is:A, D
By Rotation theory
z2z1=cosθeiθ
z3z1=cos2θcosθ.eiθ
So z22z3z1=cos2θcos2θ=32
θ=π6

Topper's Solved these Questions
Similar Questions
If P and Q are represented by the complex numbers z1 and z2 such that ∣∣∣1z2+1z1∣∣∣=∣∣∣1z2−1z1∣∣∣, then
View SolutionP is a point on the argand diagram on the circle with OP as diameter two points taken such that ∠POQ=∠QOR=0 If O is the origin and P, Q, R are are represented by complex z1,z2,z3 respectively then show that z22cos2θ=z1z3cos2θ
View Solution
Knowledge Check
If P andn Q are represented by the complex numbers z1 and z2 such that |1/z2+1/z1|=|1/z2−1/z1|, then
AΔOPQ (where O is the origin) is equilateral.BΔOPQ is right angledCthe circumcentre of ΔOPQ is 12(z1+z2)Dthe circumcentre of ΔOPQ is 12(z1−z2)If PandQ are represented by the complex numbers z1andz2 such that ∣∣∣1z2+1z1∣∣∣=∣∣∣1z2−1z1∣∣∣, then the circumstance of ΔOPQ (where O is the origin) is
A12(z1−z2)B13(z1+z2)C12(z1+z2)D13(z1−z2)Two points P and Q in the argand plane represent the complex numbers z and 3z+2+u. If |z|=2, then Q moves on the circle, whose centre and radius are (here, i2=−1)
A−2+i,6B2−i,3C2+i,6D2+i,2
If the points represented by complex numbers z1=a+ib,z2=c+z1−z2 are collinear, where i=√−1, then
View SolutionP is a point on the argand diagram on the circle with OP as diameter two points taken such that ∠POQ=∠QOR=θ. If O is the origin and P, Q, R are are represented by complex z1,z2,z3 respectively then show that z22cos2θ=z1z3cos2θ
View SolutionTwo points P and Q in the argand plane represent the complex numbers z and 3z+2+u. If |z|=2, then Q moves on the circle, whose centre and radius are (here, i2=−1)
View SolutionIf the points P and Q represent the complex numbers z and iz then ∠POQ is a right angle. State true or false
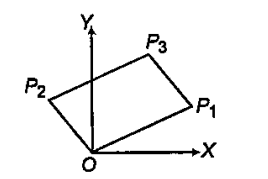
View SolutionIn a given parallelogram, if the points P1 and P2 represent two complex numbers z1 and z2, then the point P3 represents the number
View Solution
