Let $P_{1} : x + y + z = 0$
$P_{2} x + 2 y + 3 y = 0$
$P_{3} : x + 3 y + 5 z = 0$ be three planes
$L_{1}$ is the line of intersection of $P_{1} & P_{2}$
Let $P (2, 1 - 1)$ be point on $P_{3}$ If $(α, β, λ)$ is image of point P in line $L_{1}$ then value of $| α + β + λ |$ is

Text Solution

Verified by Experts

The correct Answer is:2

Direction ratio of line $L_{1}$ is $∣ ∣ ∣ ∣ ∣ \begin{matrix} ˆ i & ˆ j & ˆ k 1 & 1 & 1 1 & 2 & 3 \end{matrix} ∣ ∣ ∣ ∣ ∣$
therefore Line $L_{1} : \frac{x}{1} = \frac{y}{- 2} = \frac{z}{1}$

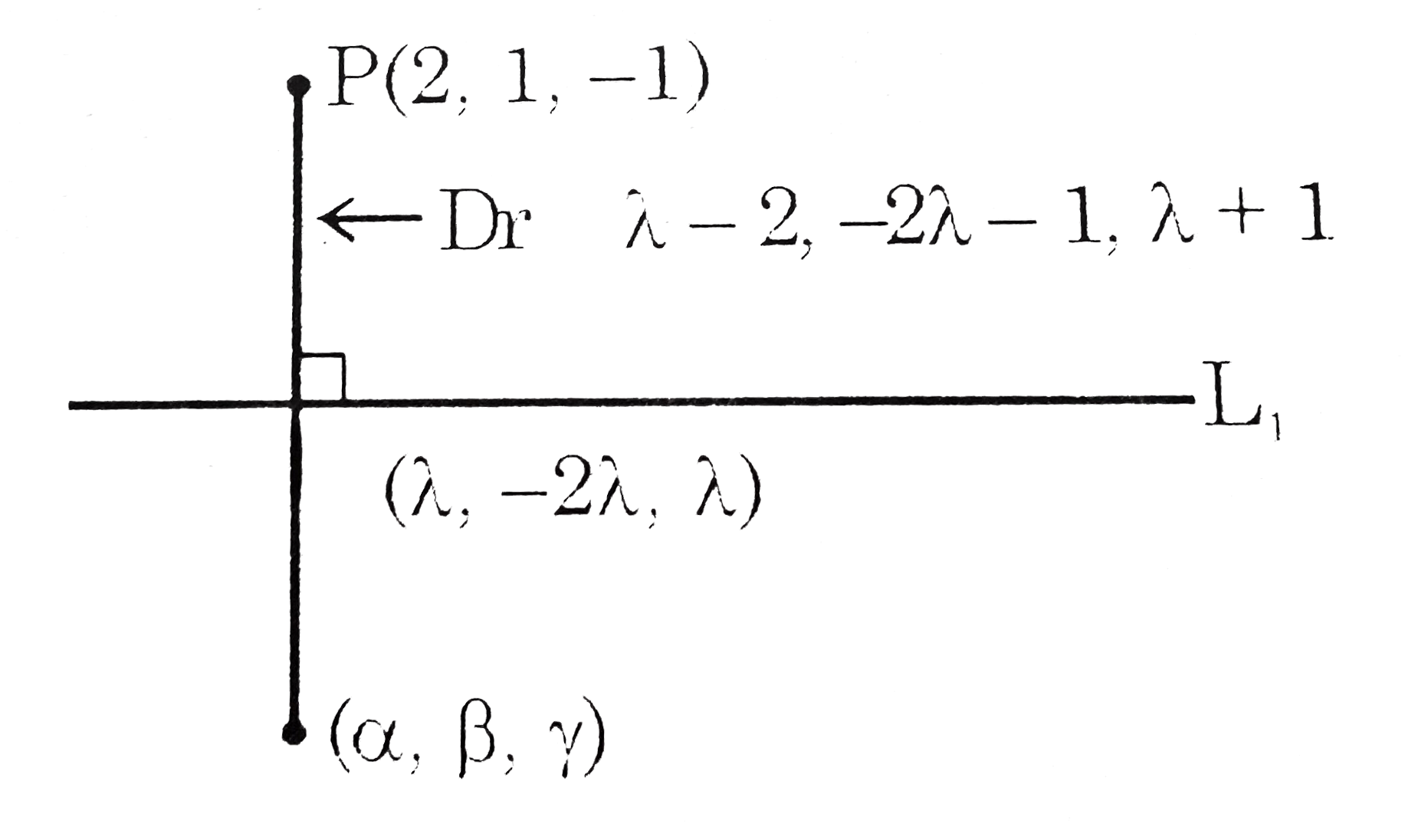
$(λ - 2) - 2 (- 2 λ - 1) + (λ + 1) 1 = 0$
$6 λ = - 1 \Rightarrow λ = \frac{- 1}{6}$
$\frac{α + 2}{2} = λ, \frac{β + 1}{2} = - 2 λ, \frac{λ - 1}{2} = λ$
$\Rightarrow α + β + λ = - 2 - 1 + 1 + 2 λ - 41 + 2 λ = - 2$

|

Updated on:21/07/2023

Class 12 MATHS QUESTION BANK

Topper's Solved these Questions

Similar Questions

Knowledge Check

Question 1 - Select One
Let $P_{1} = x + y + z + 1 = 0, P_{2} = x - y + 2 z + 1 = 0, P_{3} = 3 x + y + 4 z + 7 = 0$ be three planes. Find the distance of line of intersection of planes $P_{1} = 0$ and $P_{2} = 0$ from the plane $P_{3} = 0 .$
A $\frac{2}{\sqrt{26}}$
B $\frac{4}{\sqrt{26}}$
C $\sqrt{\frac{1}{26}}$
D $\frac{7}{\sqrt{26}}$
Question 2 - Select One
Let $P_{1} : 2 x + y + z + 1 = 0$
$P_{2} : 2 x - y + z + 3 = 0$ and $P_{3} : 2 x + 3 y + z + 5 = 0$ be three planes, then the distance of the line of intersection of planes $P_{1} = 0$ and $P_{2} = 0$ from the plane $P_{3} = 0$ is
A $\frac{3}{\sqrt{14}}$ units
B $\frac{6}{\sqrt{14}}$ units
C $\frac{3}{\sqrt{7}}$ units
D $\frac{6}{\sqrt{7}}$ units
Question 3 - Select One
$P_{1} : x + 3 y - z = 0 and P_{2}, y + 2 z = 0$ are two intersecting planes $P_{3}$ is a plane passing through the point (2,1,-1) and through the line of intersection of $P_{1} and P_{2}$

Equation of $P_{3}$ is
A4x + y - 2z = 10
Bx + y - 2z = 3
Cx + 9y + 11z = 0
D4x - y + z = 0

ALLEN-TEST PAPERS-part-2 Mathematics

Home
Ask Doubt
Profile