In the given figure PA and PB are tangents to a circle with centre O. if ∠APB=(2x+3)∘ and ∠AOB=(3x+7)∘. then find the value of x.
As tangents from an external point are perpendicular to radius of the circle,
∴∠OAP=∠OBP=90∘
Now, in quadrilateral OAPB,
∠OAP+∠APB+∠OBP+∠BOA=360∘
∠90∘+2x+3+90∘+3x+7=360∘
5x+10=180∘
x=1705
⇒x=34
Similar Questions
PA and PB are two tangents drawn to a circle with center O from an external point P. If ∠APB=30∘,then∠AOB= …….
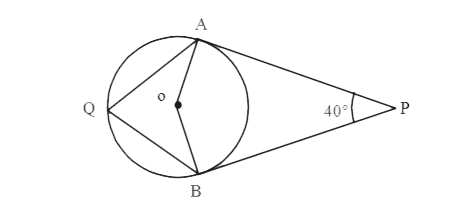
View SolutionIn the given figure, O is the centre of the circle, PA and PB are tangents to the circle then find ∠AQB.
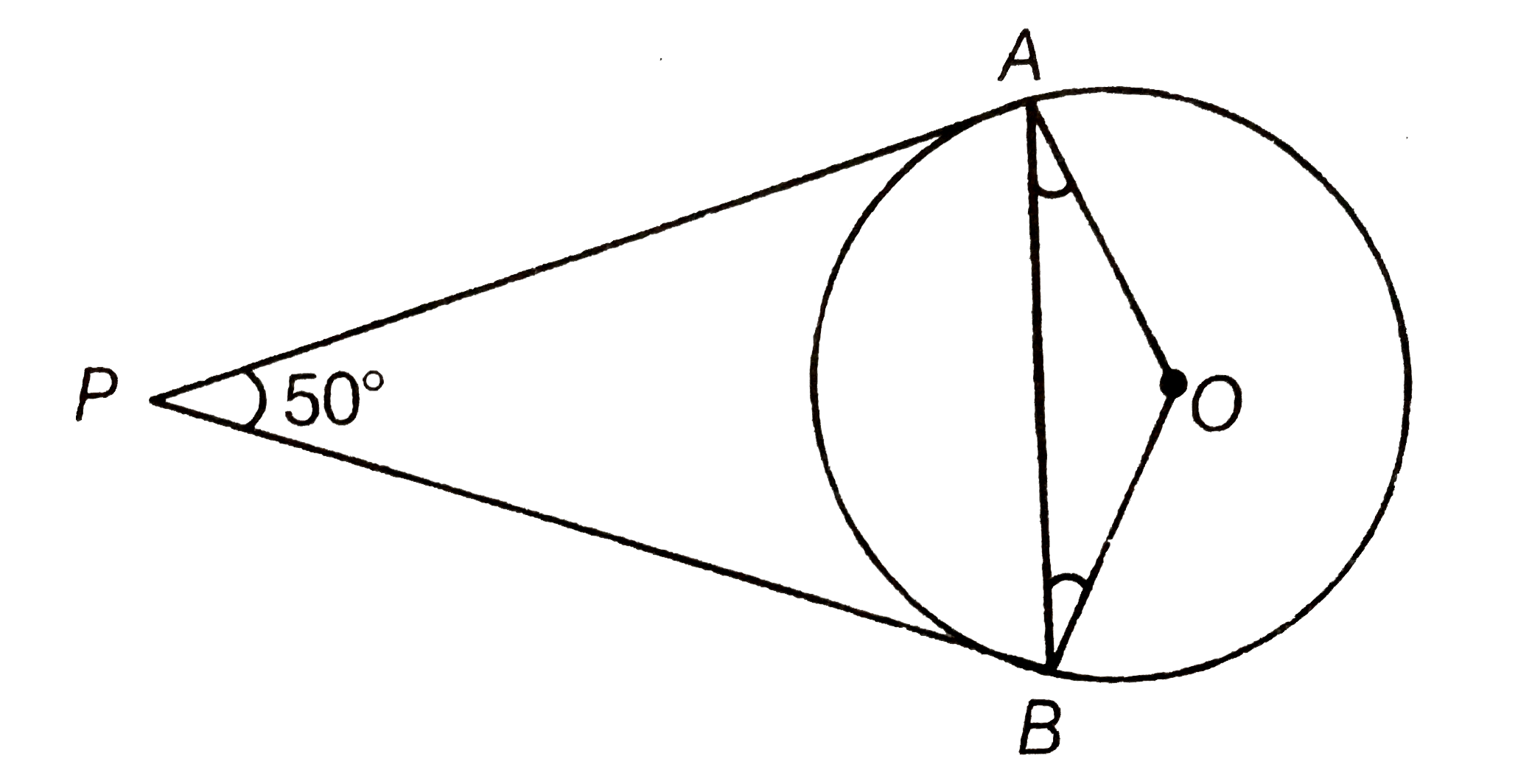
View SolutionIn figure, if PA and PB are tangents to the circle with centre O such that ∠APB=50∘, then ∠OAB is equal to
View SolutionIn the given figure, O is the centre of the circle angleAOB=90^@ Find m angleAPB
View SolutionIn the given figure, PA and PB are tangents to a circle with centre O. Prove that ∠APB and ∠AOB are supplementary.

View SolutionFrom an external point P, tangent PA=PB are drawn to a circle with centre O. If ∠PAB=50∘, then find ∠AOB.
View SolutionIf PA and PB are two tangents to a circle with center O, so that angleAOB = 110 is, then angleAPB Is
View SolutionIf PA and PB are tangents to a circle with center O such that angleAPB= 50^(@) , So angleOAB = ?
View Solution
