Rank of a Matrix
Rank of a Matrix
The rank of a matrix can be defined in two different forms and ways. One is the maximum number of linearly independent column vectors in the matrix. And another definition of the rank of a matrix can be put as the maximum number of linearly independent row vectors in the matrix. Either one of these definitions can be considered to characterize the rank of a matrix.
What is Rank of a Matrix?
To understand, the rank of matrix, let us consider a matrix with a set of r x c. This statement indicates that the matrix is having a set of ‘r’ row vectors with each row having ‘c’ elements in them, or you can consider it as a set of c column vectors, each having r elements.
For a matrix denoted by ‘r’ x ‘c’;
If r is less than c, then the maximum rank of the matrix can be said as r.
And if r is greater than c, then the maximum rank of the matrix can be said as c.
Supposing that if the matrix had no elements, then the rank of that matrix would be zero or 0.
And, supposing that the matrix had only one element, then the minimum rank of that matrix would be one or 1.
How to find the Rank of a Matrix?
In order to find the rank of any matrix in the method we propose, you need to have a proper understanding of echelon matrices and echelon transformations.
Based on the matrices concept that theories, we know that the maximum number of linearly independent vectors in a matrix will be equal to the number of non-zero rows in the row echelon matrix. Thus, in order to find the rank of any matrix, we will first simply transform that matrix into its echelon form and then determine the rank by based on the number of non zero rows.
This method is considered by many as a very popular and simplest method in determining the rank of a matrix and thereby concludes with the number of non-zero elements in the matrix as the rank of that particular matrix.
Related Videos:
- Row matrix and column matrix
- Square matrix and diagonal matrix
- Scalar matrix and identity matrix
- Null matrix upper triangular matrix and lower triangular matrix
- Symmetric matrix
- skew symmetric matrix
Rank of a Matrix Example
In figure 1, while observing the rows, it can be seen that the second row is three times just the first row. So, even though the matrix has two rows, it does not count and the rank of the matrix is only considered to be 1.

On the other hand, when observing the columns of the same given matrix, it can be seen that the second column is just two times the first column and also that the third column is thrice the first column. So, even this assortment does not count, and the rank of that matrix is only considered to be as 1.
In the next example, figure 2, even though the matrix has already three rows, the rank of the matrix cannot be given as 3. This is so because, the second row of all the three rows is not made up of the first row, and so the rank of the matrix can be at least two or 2.
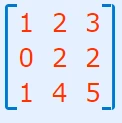
However, the third row is also there in the matrix, as can be seen. The elements of the third row are formed by adding up the elements present in the first and second rows. Hence, the third row in the matrix formed by three rows, does not count in deriving the rank of the matrix. Thus, even through the matrix have a total of three rows the rank cannot be more than 3 and will be count as two or 2.
Now, for the same example, we will look at the columns for arriving at the rank of the matrix. The second column can be considered as a fine element for arriving at the rank of the matrix. However, when we look at column 3 in the matrix, the elements of column 3 in the matrix are formed by adding up all the corresponding elements in columns 1 and 2. Therefore, column 3 does not count in the ranking of the matrix. Thus, the columns in the matrix also indicate that the rank of the matrix is two or 2.
In the third example, figure 3, we can see that the second row is not formed based on the first row. And so, the rank of the matrix can be at least two or 2. Now, on observing the third row, it can be noticed that the elements of the third row are formed by the first row deducted from two times of the second row. Thus, the rank of the matrix can be concluded as two or 2.

On observing the columns, the elements of the column 2 are formed by adding up all the elements of columns one and two summing up together, thereby forming the elements of the second column. Thus, the columns are also showing that the rank of this matrix as two or 2.
Now, when we look at an identity matrix, figure 4, when we see the elements of the rows in the identity matrix, it is observed that the elements of the rows in the matrix are strong independent individuals without showing any reliance on their existence. Thus, the rank of this identity matrix as three or 3.
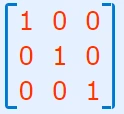
The same phenomenon can be observed with the elements present in the construction of the elements in the columns and so, the rank of the matrix through observing the elements in the columns as number three or 3.
Now that we can conclude that the on observing the elements of the matrix through rows and columns, it can be concluded that the rank can be easily determined through observing the elements structured in the matrix.
Important Chapters:




Similar Questions
Knowledge Check
The rank of the matrix A=[12344321], is
A1B2C3D4The rank of the matrix A=⎡⎢⎣123369123⎤⎥⎦, is
A1B2C3Dnone of these
The rank of the matrix A=[−123−246] is
View SolutionFind the rank of the matrix [10−42−13]
View SolutionFind the rank of the matrix A=⎡⎢⎣123234345⎤⎥⎦.
View SolutionThe rank of the matrix A=⎡⎢⎣123456345⎤⎥⎦ is
View SolutionFind the rank of the matrix ⎡⎢⎣123223511345⎤⎥⎦
View SolutionFind the rank of the matrix ⎡⎢⎣023046069⎤⎥⎦
View Solution
