Two blocks of mass m1andm2 are moving along a smooth horizontal floor. A non-ideal spring is attached at the back of mass m2. Initial velocities of the blocks are u1andu2 as shown, with u1>u2. After collision the two blocks were found to be moving with velocities V1andV2 respectively. Find the ratio of impulse (on each block) during the deformation phase of the spring and that during its restoration phase. [By non ideal spring we mean that it does not completely regain its original shape after deformation. You can neglect the mass of the spring.]
![Two blocks of mass m(1) and m(2) are moving along a smooth horizontal floor. A non-ideal spring is attached at the back of mass m(2). Initial velocities of the blocks are u(1) and u(2) as shown, with u(1) gt u(2). After collision the two blocks were found to be moving with velocities V(1) and V(2) respectively. Find the ratio of impulse (on each block) during the deformation phase of the spring and that during its restoration phase. [By non ideal spring we mean that it does not completely regain its original shape after deformation. You can neglect the mass of the spring.]](https://d10lpgp6xz60nq.cloudfront.net/physics_images/IJA_PHY_V01_C05_E01_020_Q01.png)
The correct Answer is:u1−u2V2−V1
Step by step video, text & image solution for Two blocks of mass m_(1) and m_(2) are moving along a smooth horizontal floor. A non-ideal spring is attached at the back of mass m_(2). Initial velocities of the blocks are u_(1) and u_(2) as shown, with u_(1) gt u_(2). After collision the two blocks were found to be moving with velocities V_(1) and V_(2) respectively. Find the ratio of impulse (on each block) during the deformation phase of the spring and that during its restoration phase. [By non ideal spring we mean that it does not completely regain its original shape after deformation. You can neglect the mass of the spring.] by Physics experts to help you in doubts & scoring excellent marks in Class 11 exams.
Updated on:21/07/2023Topper's Solved these Questions
Similar Questions
Block of mass m1 moving on a smooth horizontal surface,collides with a stationary block of mass m2 .The coefficient of restitution for the collision is e.The ratio m1m2 for which m1 is at rest after collision is
View SolutionTwo blocks of mass m1andm2 lie on smooth horizontal table in contact with each other as shown in figure
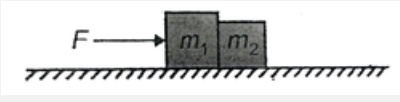
If a force F is applied to the mass m1 then the contact force between the block will be
View Solution
Knowledge Check
In fig., blocks A and B move with velocities v1 and v2 along horizontal direction. Find the ratio of v1/v2
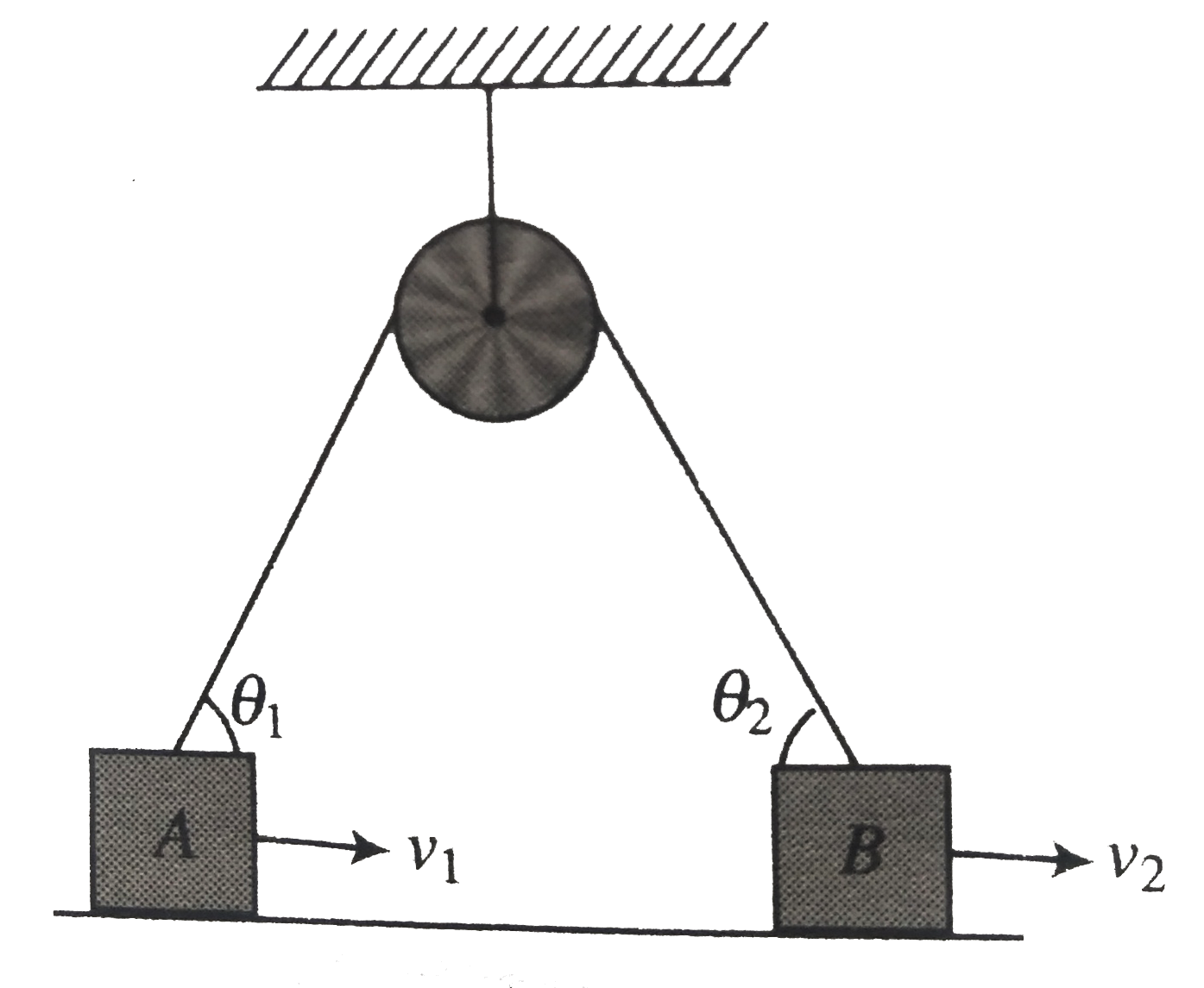 Asinθ1sinθ2Bsinθ2sinθ1Ccosθ2cosθ1Dcosθ1cosθ2
Asinθ1sinθ2Bsinθ2sinθ1Ccosθ2cosθ1Dcosθ1cosθ2Two block of masses m1 and m2 are connected as shown in the figure. The acceleration of the block m2 is:
 Am2gm1+m2Bm1gm1+m2C4m2g−m1gm1+m2Dm2gm1+4m2
Am2gm1+m2Bm1gm1+m2C4m2g−m1gm1+m2Dm2gm1+4m2Two particles of same mass m moving with velocities u1 and u2 collide perfectly inelastically. The loss of energy would be :
A1/2m(u1−u2)2B1/4m(u1−u2)2Cm(u1−u2)2D2m(u1−u2)2
Two spheres made of clay of masses 'm1' and 'm2' moving along a straight line in the same direction collide with each other. Their velocities just before collision are 'u1' and 'u2' respectively. After collision, they stick together and move with teh same velocity, in the same direction, along the straight line. Find the velocity with which they move together.
View Solution[" Block of mass "m_(1)" moving on a smooth "],[" horizontal surface,collides with a "],[" stationary block of mass "m_(2)" .The "],[" coefficient of restitution for the "],[" collision is e.The ratio "(m_(1))/(m_(2))" for which "m_(1)],[" is at rest after collision is "]
View SolutionTwo blocks of masses 1kg and 3kg are moving with velocities 2m/s and 1m/s , respectively , as shown. If the spring constant is 75N/m , the maximum compression of the spring is

View SolutionTwo blocks, with masses m12.5kg and m2=14kg, approach each other along a horizontal, frictionless track, The initial velocities of the blocks are v1=12.0m/s to the right an dv2=3.4m/s to the left. The two blocks then collide and stick together. Which of the graph could represent the force of block 1 on block 2 during the collision ?
View SolutionTwo identical mass M moving with velocity u1andu2 collide perfectly inelastically. The loss in kinetic energy is
View Solution
