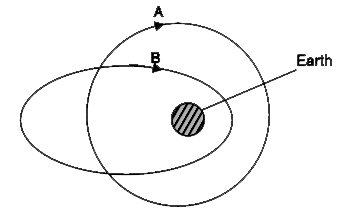
Satellite A is following a circular path of radius a around the earth another satellite B follows an elliptical path around the earth. The two satellites have same mechanical energy and their orbits intersect. Find the speed of satellite B at the point where its path intersects with the circular orbit of A. Take mass of earth to be M.

Text Solution

Verified by Experts

The correct Answer is: $\sqrt{\frac{G M}{a}}$

|

Updated on:21/07/2023

Class 11 PHYSICS GRAVITATION

Topper's Solved these Questions

Similar Questions

Knowledge Check

Question 1 - Select One
A satellite is revolving in circular orbit of radius $r$ around the earth of mass M. Time of revolution of satellite is
A $T \propto \frac{r^{5}}{G M}$
B $T \propto \sqrt{\frac{r^{3}}{G M}}$
C $T \propto \sqrt{\frac{r}{\frac{G M^{2}}{3}}}$
D $T \propto \sqrt{\frac{r^{3}}{\frac{G M}{4}}}$
Question 2 - Select One or More
A satellite S is moving in an elliptical orbit around the earth. The mass of the satellite is very small compared to the mass of the earth.
AThe acceleration of S is always directin towards the centre of the earth.
BThe angular momentum of S about the centre of the earth changes in direction, but its magnitude remains constant.
CThe total mechanical energy of S varies periodically with time.
DThe linear momentum of S remains constant in magnitde.
Question 3 - Select One
A satellite goes along an elliptical path around earth. The rate of change of area swept by the line joining earth and the satellite is proportional to
A $r^{\frac{1}{2}}$
B $r$
C $r^{\frac{3}{2}}$
D $r^{2}$

ARIHANT-GRAVITATION-Exercise

Home
Ask Doubt
Profile