A solid wooden cone has been supported by a string inside water as shown in the figure. The radius of the circular base of the cone is R and the volume of the cone is v. In equilibrium the base of the cone is at a depth H below the water surface. Density of wood is d(<ρ, density of water).
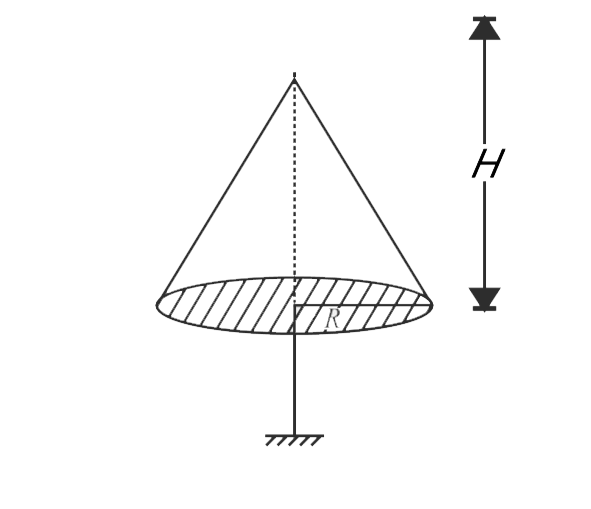
(a) Find tension in the string.
(b) Find the force applied by the water on the slant surface of the coone. take atmospheric pressure to be p0.
The correct Answer is:(a) vg(d−ρ)
(b) πR2(ρ0+ρgH)−vρg
Step by step video, text & image solution for A solid wooden cone has been supported by a string inside water as shown in the figure. The radius of the circular base of the cone is R and the volume of the cone is v. In equilibrium the base of the cone is at a depth H below the water surface. Density of wood is d(ltrho, density of water). (a) Find tension in the string. (b) Find the force applied by the water on the slant surface of the coone. take atmospheric pressure to be p_(0). by Physics experts to help you in doubts & scoring excellent marks in Class 11 exams.
Topper's Solved these Questions
Similar Questions
Knowledge Check
- Question 1 - Select One
A solid wooden cone has been supported by a string inside water as shown in the figure. The radius of the circular base of the cone is R and the volume of the cone is V. In equilibrium the base of the cone is at a depth H below the water surface. Density of wood is d(<ρ, density of water) Then tension in the string is
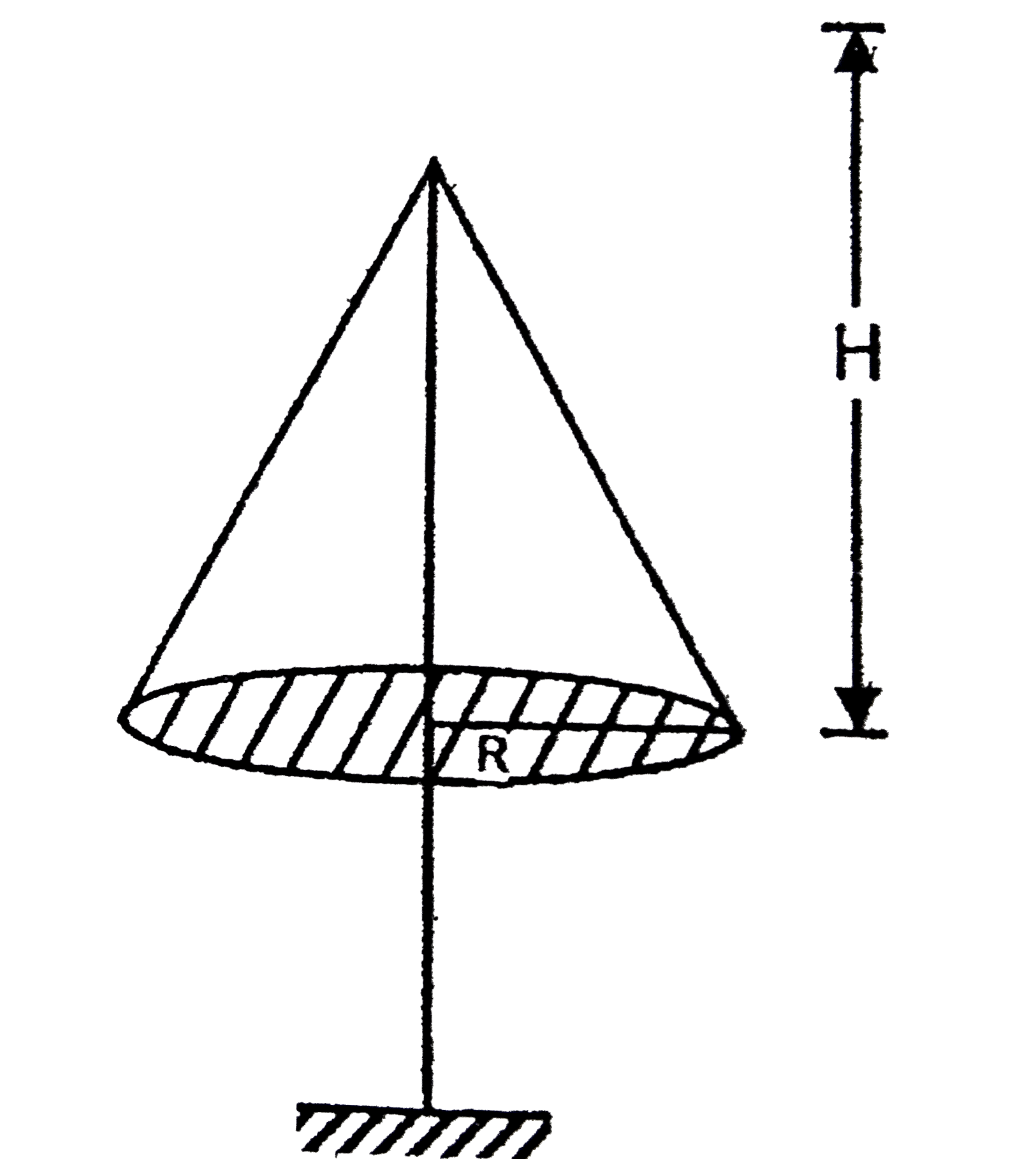 AVg(ρ−d)BVg(d+ρ)C2Vg(ρ−d)DNone of these
AVg(ρ−d)BVg(d+ρ)C2Vg(ρ−d)DNone of these - Question 2 - Select One
The radius of a circular cone is R and its height is H. The volume of cone is :
AπR2HB23πR2HCπR2H3DπRH2 - Question 3 - Select One
The radius of the base of a cone is 21 cm and the height is 20 cm. Find the volume the cone
A8460cm3B9240cm3C4620cm3D3230cm3
The area of the base of a right circular cone is 314cm2 and its height is 15cm. Find the volume of the cone.
View SolutionThe radius of the base and the height of a right circular cone are doubled. The volume of the cone will be
View SolutionThe radius of the base of a solid right circular cone is 8 cm and its height is 15 cm. The total surface area of the cone is:
View SolutionThe radius of the base of a right circular cone is doubled. To keep the volume fixed, the height of the cone will be
View SolutionIf the radius of the base of a cone be 7 cm and its curved surface area be 550 sq. cm, then the volume of the cone is
View Solution

