A rectangular bar is fixed to a hard floor. Height of the bar is h and its area in contact with the floor is A. A shearing force distorts the bar as shown. Prove that the work done by the shearing force is W=(σ22η)× volume of the bar. Here σ is shear modulus of elasticity. Assume the deformation to be small.
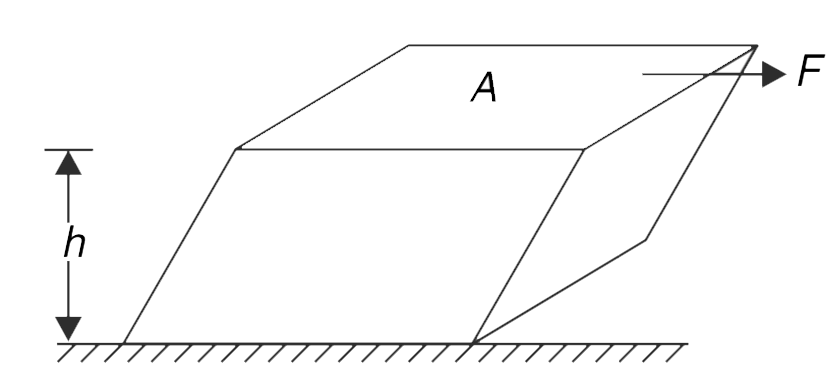
Step by step video, text & image solution for A rectangular bar is fixed to a hard floor. Height of the bar is h and its area in contact with the floor is A. A shearing force distorts the bar as shown. Prove that the work done by the shearing force is W = ((sigma^(2))/(2 eta)) xx volume of the bar. Here sigma is shear modulus of elasticity. Assume the deformation to be small. by Physics experts to help you in doubts & scoring excellent marks in Class 11 exams.
Topper's Solved these Questions
- BOOK - ARIHANTCHAPTER - ELASTICITYEXERCISE - Level 31videos
ELASTICITY
- BOOK - ARIHANTCHAPTER - ELASTICITYEXERCISE - Level 31videos
ELASTICITY
- BOOK - ARIHANTCHAPTER - CALORIMETRYEXERCISE - Level 31videos
CALORIMETRY
- BOOK - ARIHANTCHAPTER - FIRST LAW OF THERMODYNAMICSEXERCISE - Level 36videos
FIRST LAW OF THERMODYNAMICS
Similar Questions
The brick shown in the figure is glued to the floor. A 3500 N force is applied to the top surface of the brick as shown. If the brick has a shear modulus of 5.4×109N/m2, how far to the right does the top face move relative to the stationary bottom face
 View Solution
View SolutionA bar is subjected lu axial forces as shown. is the modulus of elasticity of the bar is E and A is it cross-section area. Its elongation will be
 View Solution
View Solution
Knowledge Check
- Question 1 - Select One
A rectangular bar is uniformly loaded axially with force per unit area σ shown. Shown is a section AA' in the bar. Normal stress for the section is
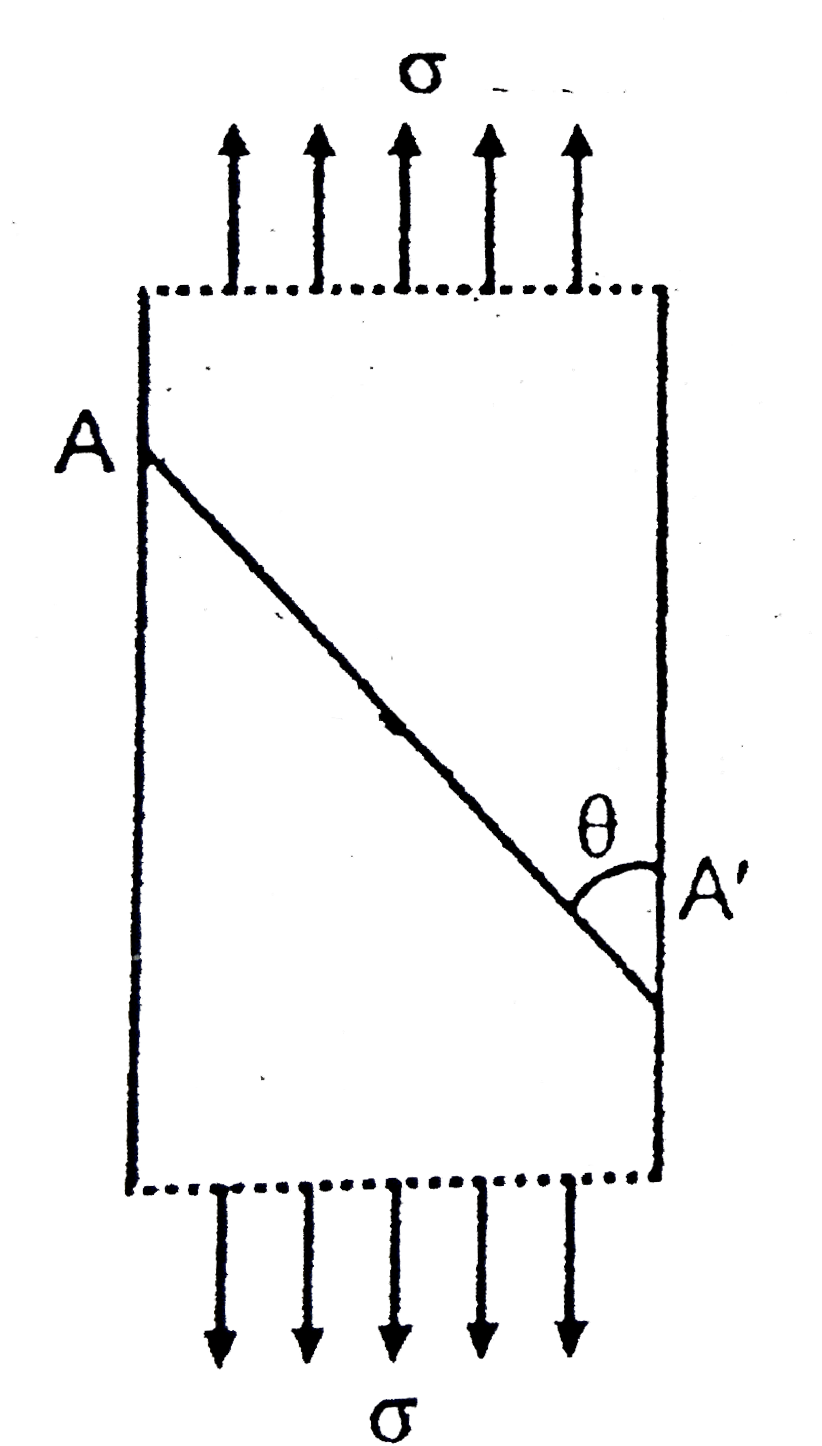 AσsinθBσCσsin2θDσsinθcosθ
AσsinθBσCσsin2θDσsinθcosθ - Question 2 - Select One
A force ¯¯¯F=(¯5I+¯3j+2¯k)N is applied over a particle which displaces it from its original to the point ¯t=(2¯i−¯j)m. The work done the particle in joules is
A+10B+7C−7D+13
A bar of cross section A is subjected to equal and opposite tensile forces F at its ends. Consider a plane through the bar making an angle θ with a plane at right angles to the bar as shown in figure.
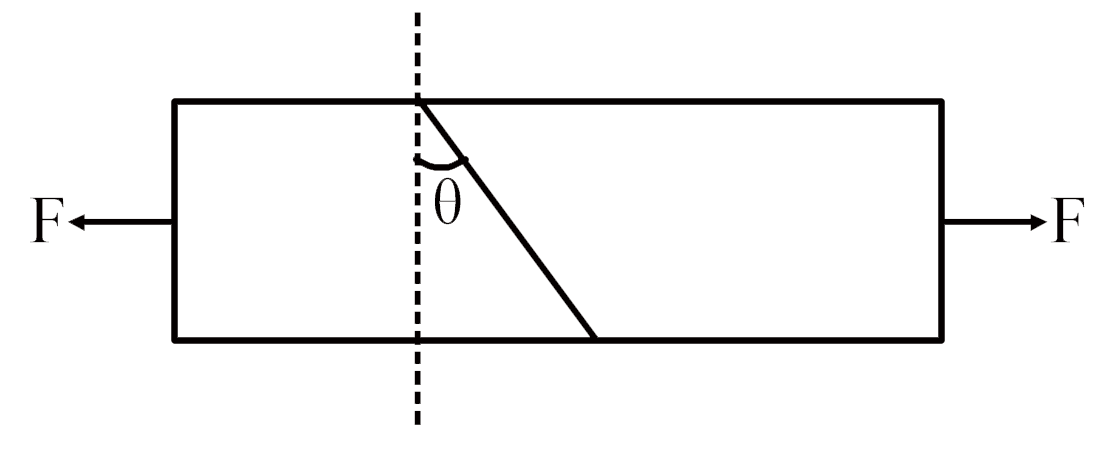
The shearing stress at the plane, in terms of F, A and θ isView SolutionThe word fluid means a substance having particles which readily of its magnitude (a small shear stress, which may appear to be of negligible will cause deformation in the fluid). Fluids are charactrised by such properties as density. Specific weight, specific gravity, viscosity etc. Density of a substance is defined as mass per unit volume and it is denoted by. The specific gravity represents a numerical ratio of two densities, and water is commonly taken as a reference substance. Specific gravity of a substance in written as the ratio of density of substance to the density of water. Specific weight represents the force exerted by gravity on a unit volume of fluid. It is related to the density as the product of density of a fluid and acceleration due to gravity. Viscosity is the most important and is recognized as the only single property which influences the fluid motion to a great extent. The viscosity is the property by virtue of which a fluid offers resistance to deformation under the influenece if shear force. The force between the layers opposing relative motion between them are known as forces of viscosity. When a boat moves slowly on the river remains at rest. Velocities of different layers are different. Let v be the velocity of the level at a distance y from the bed and V+dv be the velocity at a distance y+dy. The velocity differs by dv in going through a distance by perpendicular to it. The quantity dvdy is called velocity gradient. The force of viscosity between two layers of a fluid is proportional to velocity gradient and Area of the layer.
F∝A & F∝dvdy
F=−ηAdvdy (−ve sign shown the force is frictional in nature and opposes relative motion. η coefficient of dynamic viscosity
Shear stress FA=−ηdvdy
and simultaneously kinematic viscosity is defined as the dynamic viscosity divided by the density. If is denoted as v. The viscosity of a fluid depends upon its intermolecular structure. In gases, the molecules are widely spaced resulting in a negligible intermolecular cohesion, while in liquids the molecules being very close to each other, the cohesion is much larger with the increases of temperature, the cohesive force decreases rapidly resulting in the decreases of viscosity. In case of gases, the viscosity is mainly due to transfer of molecular momentum in the transerve direction brought about by the molecular agitation. Molecular agitation increases with rise in temperature. Thus we conclude that viscosity of a fluid may thus be considered to be composed of two parts, first due to intermolecuar cohesion and second due to transfer of molecular momentum.
If the velocity profile is given by
v=23y−y2v is velocity in m/secy is in meter above the bad. Determine shear stress at y=0.15m, & η=0.863Ns/m2View SolutionThe word fluid means a substance having particles which readily of its magnitude (a small shear stress, which may appear to be of negligible will cause deformation in the fluid). Fluids are charactrised by such properties as density. Specific weight, specific gravity, viscosity etc. Density of a substance is defined as mass per unit volume and it is denoted by. The specific gravity represents a numerical ratio of two densities, and water is commonly taken as a reference substance. Specific gravity of a substance in written as the ratio of density of substance to the density of water. Specific weight represents the force exerted by gravity on a unit volume of fluid. It is related to the density as the product of density of a fluid and acceleration due to gravity. Viscosity is the most important and is recognized as the only single property which influences the fluid motion to a great extent. The viscosity is the property by virtue of which a fluid offers resistance to deformation under the influenece if shear force. The force between the layers opposing relative motion between them are known as forces of viscosity. When a boat moves slowly on the river remains at rest. Velocities of different layers are different. Let v be the velocity of the level at a distance y from the bed and V+dv be the velocity at a distance y+dy. The velocity differs by dv in going through a distance by perpendicular to it. The quantity dvdy is called velocity gradient. The force of viscosity between two layers of a fluid is proportional to velocity gradient and Area of the layer.
F∝A & F∝dvdy
F=−ηAdvdy (−ve sign shown the force is frictional in nature and opposes relative motion. η coefficient of dynamic viscosity
Shear stress FA=−ηdvdy
and simultaneously kinematic viscosity is defined as the dynamic viscosity divided by the density. If is denoted as v. The viscosity of a fluid depends upon its intermolecular structure. In gases, the molecules are widely spaced resulting in a negligible intermolecular cohesion, while in liquids the molecules being very close to each other, the cohesion is much larger with the increases of temperature, the cohesive force decreases rapidly resulting in the decreases of viscosity. In case of gases, the viscosity is mainly due to transfer of molecular momentum in the transerve direction brought about by the molecular agitation. Molecular agitation increases with rise in temperature. Thus we conclude that viscosity of a fluid may thus be considered to be composed of two parts, first due to intermolecuar cohesion and second due to transfer of molecular momentum.
Viscosity of liquidsView SolutionThe word fluid means a substance having particles which readily of its magnitude (a small shear stress, which may appear to be of negligible will cause deformation in the fluid). Fluids are charactrised by such properties as density. Specific weight, specific gravity, viscosity etc. Density of a substance is defined as mass per unit volume and it is denoted by. The specific gravity represents a numerical ratio of two densities, and water is commonly taken as a reference substance. Specific gravity of a substance in written as the ratio of density of substance to the density of water. Specific weight represents the force exerted by gravity on a unit volume of fluid. It is related to the density as the product of density of a fluid and acceleration due to gravity. Viscosity is the most important and is recognized as the only single property which influences the fluid motion to a great extent. The viscosity is the property by virtue of which a fluid offers resistance to deformation under the influenece if shear force. The force between the layers opposing relative motion between them are known as forces of viscosity. When a boat moves slowly on the river remains at rest. Velocities of different layers are different. Let v be the velocity of the level at a distance y from the bed and V+dv be the velocity at a distance y+dy. The velocity differs by dv in going through a distance by perpendicular to it. The quantity dvdy is called velocity gradient. The force of viscosity between two layers of a fluid is proportional to velocity gradient and Area of the layer.
F∝A & F∝dvdy
F=−ηAdvdy (−ve sign shown the force is frictional in nature and opposes relative motion. η coefficient of dynamic viscosity
Shear stress FA=−ηdvdy
and simultaneously kinematic viscosity is defined as the dynamic viscosity divided by the density. If is denoted as v. The viscosity of a fluid depends upon its intermolecular structure. In gases, the molecules are widely spaced resulting in a negligible intermolecular cohesion, while in liquids the molecules being very close to each other, the cohesion is much larger with the increases of temperature, the cohesive force decreases rapidly resulting in the decreases of viscosity. In case of gases, the viscosity is mainly due to transfer of molecular momentum in the transerve direction brought about by the molecular agitation. Molecular agitation increases with rise in temperature. Thus we conclude that viscosity of a fluid may thus be considered to be composed of two parts, first due to intermolecuar cohesion and second due to transfer of molecular momentum.
Ten litres of a liquid of specific gravity 1.3 is mixed with 6 litres of a liquid of specific gravity 0.8 the specific gravity of mixture isView SolutionA steel rod of cross-sectional area Im2 is acted upon by forces as shown in the Fig. Determine the total elongation of the bar. Take Y=2.0×1011N/m2
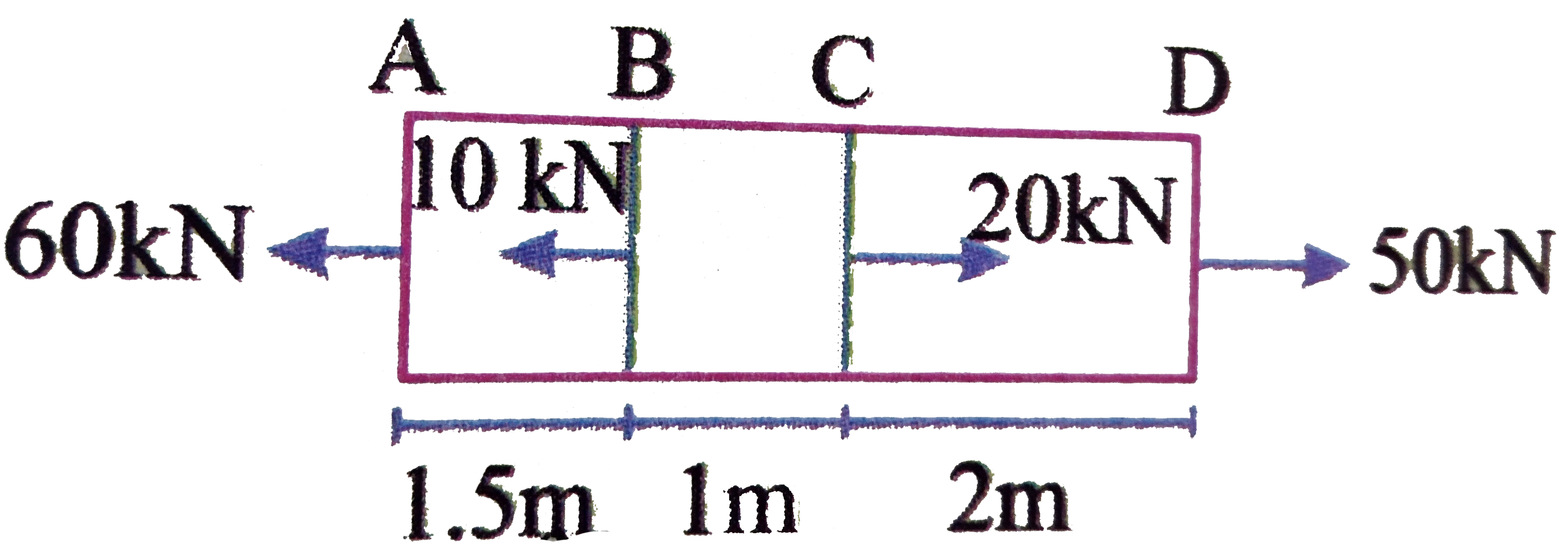 View Solution
View SolutionA box B of mass M hangs from an ideal spring of force constant k. A small particle, also of mass M, is stuck to the ceiling of the box and the system is in equilibrium. The particle gets detached from the ceiling and falls to strike the floor of the box. It takes time t for the particle to hit the floor after it gets detached from the ceiling. The particle, on hitting the floor, sticks to it and the system thereafter oscillates with a time period T. Find the height H of the box if it is given that t=T6√2. Assume that the floor and ceiling of the box always remian horizontal.
 View Solution
View Solution

