A syringe has two cylindrical parts of cross sectional area A1=4cm2 and A2=1cm2. A mass less piston can slide on the inner wall of the part having cross section A1. The end of the part having cross section A2 is open. Syringe is dipped in a large water tank such that the narrower part remains completely submerged and the wider part is filled with air. The length shown in figure are h1=55cm and h2=100 cm. The piston is pushed down by a distance x such that 25% of the air inside the syringe is expelled out through the open end of the narrower part. Assume that the temperature of air remains constant and calculate x.
Density of water = 103kgm–3,g=10ms–2, Atmospheric pressure = 105Nm–2.
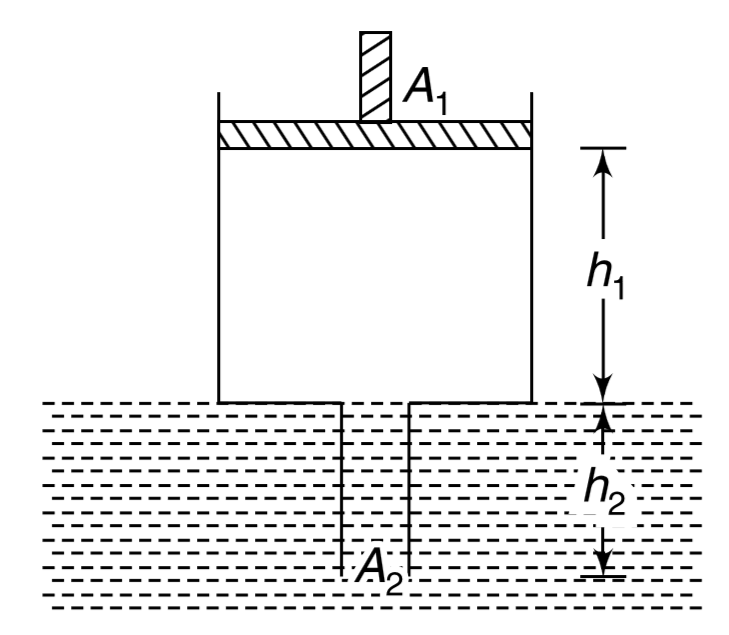
The correct Answer is:42.5 cm
Step by step video, text & image solution for A syringe has two cylindrical parts of cross sectional area A_(1) = 4 cm^(2) and A_(2) = 1 cm^(2). A mass less piston can slide on the inner wall of the part having cross section A_(1). The end of the part having cross section A_(2) is open. Syringe is dipped in a large water tank such that the narrower part remains completely submerged and the wider part is filled with air. The length shown in figure are h_(1) = 55 cm " and " h_(2) = 100 cm. The piston is pushed down by a distance x such that 25% of the air inside the syringe is expelled out through the open end of the narrower part. Assume that the temperature of air remains constant and calculate x. Density of water = 10^(3) k gm^(– 3) , g = 10 ms^(– 2), Atmospheric pressure = 10^(5) Nm^(–2). by Physics experts to help you in doubts & scoring excellent marks in Class 11 exams.
Updated on:21/07/2023Topper's Solved these Questions
- KINETIC THEORY OF GASESBOOK - ARIHANTCHAPTER - KINETIC THEORY OF GASESEXERCISE - Level 3
4 Videos
- KINETIC THEORY OF GASESBOOK - ARIHANTCHAPTER - KINETIC THEORY OF GASESEXERCISE - Level 3
4 Videos
- KINEMATICSBOOK - ARIHANTCHAPTER - KINEMATICSEXERCISE - Level 3
33 Videos
- MOMENTUM AND CENTRE OF MASSBOOK - ARIHANTCHAPTER - MOMENTUM AND CENTRE OF MASSEXERCISE - Momentum And Center of Mass
117 Videos
Similar Questions
In the given cross-section: CE = 20 cm, BC = 25 cm, AB = GF = 13 cm, AG = 10 cm and AN = 12 cm
The perimeter of the trapezium part of the cross section, is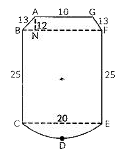
View SolutionAt the mount of the tap area of cross-section is 2.0cm2 and the speed of water is 3m/s. The area of cross-section of the water column 80 cm below the tap is (use g=10m/s2)
View Solution
Knowledge Check
A piston of cross-sectional area 100cm2 is used in a hydraulic pressure to exert a force of 107 dyne on the water. The cross-sectional area of the other piston which support a truck of mass 2000 kg is
A100cm2B109cm2C1.96×104cm2D2×1010cm2From a horizontal tube with area of cross-section A1 and A2 as shosn in fiugre liquid is flowing in the level of the liauid in the two veritcal tunes is h.
 AThe volume of the liquid flowing through the tube in time is A1v1Bv2−v1=√2ghCv22−v11=2ghDThe energy per unit mass of the liquid is the same in both sections of the tube
AThe volume of the liquid flowing through the tube in time is A1v1Bv2−v1=√2ghCv22−v11=2ghDThe energy per unit mass of the liquid is the same in both sections of the tubeA piston of cross-sectional area 100cm2 is used in a hydraulic pressure to exert a force of 107 dyne on the water. The cross-sectional area of the other piston which support a truck of mass 2000 kg is
A9.8×102cm2B9.8×103cm2C1.96×103cm2D1.96×104cm2
In the given cross-section: CE = 20 cm, BC = 25 cm, AB = GF = 13 cm, AG = 10 cm and AN = 12 cm
The area of the semi- circular part of the cross section, is
View SolutionIn the given cross-section: CE = 20 cm, BC = 25 cm, AB = GF = 13 cm, AG = 10 cm and AN = 12 cm
The perimeter of the rectangular part of the cross section, is
View SolutionThe self inductance of a solenoid that has a cross-sectional area of 1cm2, a length of 10 cm and 1000 turns of wire is
View SolutionTwo solid conductors are made up of same material have same length and same resistance . One of them has circular crosssection of area A1 and other one has square cross section of area A2. RATIO A1A2
View SolutionIf cross- sectional area of limb I is A1 and that of limb II is A2 then velocity of the liquid in the tube will be, (cross- sectional area of tube is very small)

View Solution
