(a) A charge particle travelling along positive x direction with speed Vx enters a region of width having a uniform electric field E in positive y direction. A screen is kept, at a distance D(>>l) from the region of the field, in yz plane. Find the y co-ordinate of the point where the particle strikes the screen. Charge and mass of the par- ticle is + q and m respectively.
(b) The electric field in the region is replaced with a uniform magnetic field B in negative z direction. Now calculate the y co-ordinate of the point on the screen where the particle hits it. Assume deflection due to field to be small and D>>l.
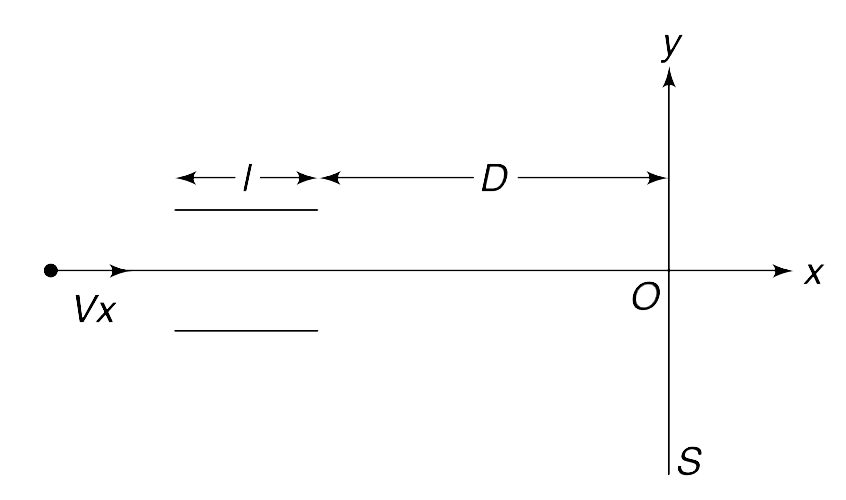
(c) Now the field region is filled with a uniform electric (E) and magnetic field (B) both directed in positive y direction. A beam of protons and some other positive ion enters the region trav- elling along x direction. The particles hit the screen along two curved paths. Explain. Draw the two curves in yz plane and point out which one represents the protons.
The correct Answer is:(a)y=qElDmV2x" "(b) y= (DlqB)/(mV_(x))
(##IJAPHYV02C09E01030_A01##)
Step by step video, text & image solution for (a) A charge particle travelling along positive x direction with speed V_(x) enters a region of width having a uniform electric field E in positive y direction. A screen is kept, at a distance D (gtgtl) from the region of the field, in yz plane. Find the y co-ordinate of the point where the particle strikes the screen. Charge and mass of the par- ticle is + q and m respectively. (b) The electric field in the region is replaced with a uniform magnetic field B in negative z direction. Now calculate the y co-ordinate of the point on the screen where the particle hits it. Assume deflection due to field to be small and Dgtgtl. (c) Now the field region is filled with a uniform electric (E) and magnetic field (B) both directed in positive y direction. A beam of protons and some other positive ion enters the region trav- elling along x direction. The particles hit the screen along two curved paths. Explain. Draw the two curves in yz plane and point out which one represents the protons. by Physics experts to help you in doubts & scoring excellent marks in Class 12 exams.
Updated on:21/07/2023Topper's Solved these Questions
- MOTION OF CHARGE IN MAGNETIC FIELDBOOK - ARIHANTCHAPTER - MOTION OF CHARGE IN MAGNETIC FIELDEXERCISE - Level-2
13 Videos
- MAGNETIC EFFECT OF CURRENTBOOK - ARIHANTCHAPTER - MAGNETIC EFFECT OF CURRENTEXERCISE - Magnetic effect of Current
45 Videos
- NUCLEAR PHYSICSBOOK - ARIHANTCHAPTER - NUCLEAR PHYSICSEXERCISE - All Questions
54 Videos
Similar Questions
A charged particle moving along +ve x-direction with a velocity v enters a region where there is a uniform magnetic field B0(−ˆk),omx=0→x=d. The particle gets deflected at an angle θ from its initial path. The specific charge of the particle is

View SolutionA n electrically charged particle enters into a uniform magnetic induction field in a direction perpendicular to the field with a velocity v then it travels
View Solution
Knowledge Check
A charged particle (charge q, mass m) has velocity v0 at origin in +x direction. In space there is a uniform magnetic field B in -z direction. Find the y coordinate of particle when is crosses y axis.
Amv0qBB2mv0qBCmv02qBDNone of theseA positively charge particle moving along x-axis with a certain velocity enters a uniform electric field directed along positively y-axis. Its
AVertical velocity changes but horizontal velocity remains constantBHorizontal velocity changes but vertical velocity remiand constantCBoth vertical and horizontal velocities changeDNeither vertical nor horizontal velocity changes.A charge particle travels along a straight line with a speed v in region where both electric field E and magnetic field b are present.It follows that
A|E|=|B| and the two field are perpendicularB|E|=v|B| and the two field are perpendicularC|B|=v|E| and the two field are parallelD|B|=v|E| and the two fields are perpendicular
Positively charged particles are projected into a magnetic field. If the direction of the magnetic field is along the direction of motion of the charged particles, the particles get
View SolutionA charged particle begins to move from the origin in a region which has a uniform magnetic field in the x-direction and a uniform electric field in the y-direction. Its speed is v when it reaches the point (x, y, z). Then, v will depend
View SolutionAn electron moving with a uniform velocity along the positive x-direction enters a magnetic field directed along the positive y-direction. The force on the electron is directed along
View SolutionA particle of charge q and mass m moving with a velocity v along the x-axis enters the region x>0 with uniform magnetic field B along the ˆk direction. The particle will penetrate in this region in the x-direction upto a distance d equal to
View SolutionA particle having mass m, charge q enters a cylindrical region having uniform magnetic field B in the inward direction as shown. If the particle is deviated by 60∘ as it emerges out of the field then what is the time spent by it in the field?
View Solution
