Electric field in a region is given by $\vec{E} = - 4 x \hat{i} + 6 y \hat{j}$ . The charge enclosed in the cube of side $1 m$ oriented as shown in the diagram is given by $α \in_{0}$ . Find the value of $α$ .

Video Solution

Text Solution

Verified by Experts

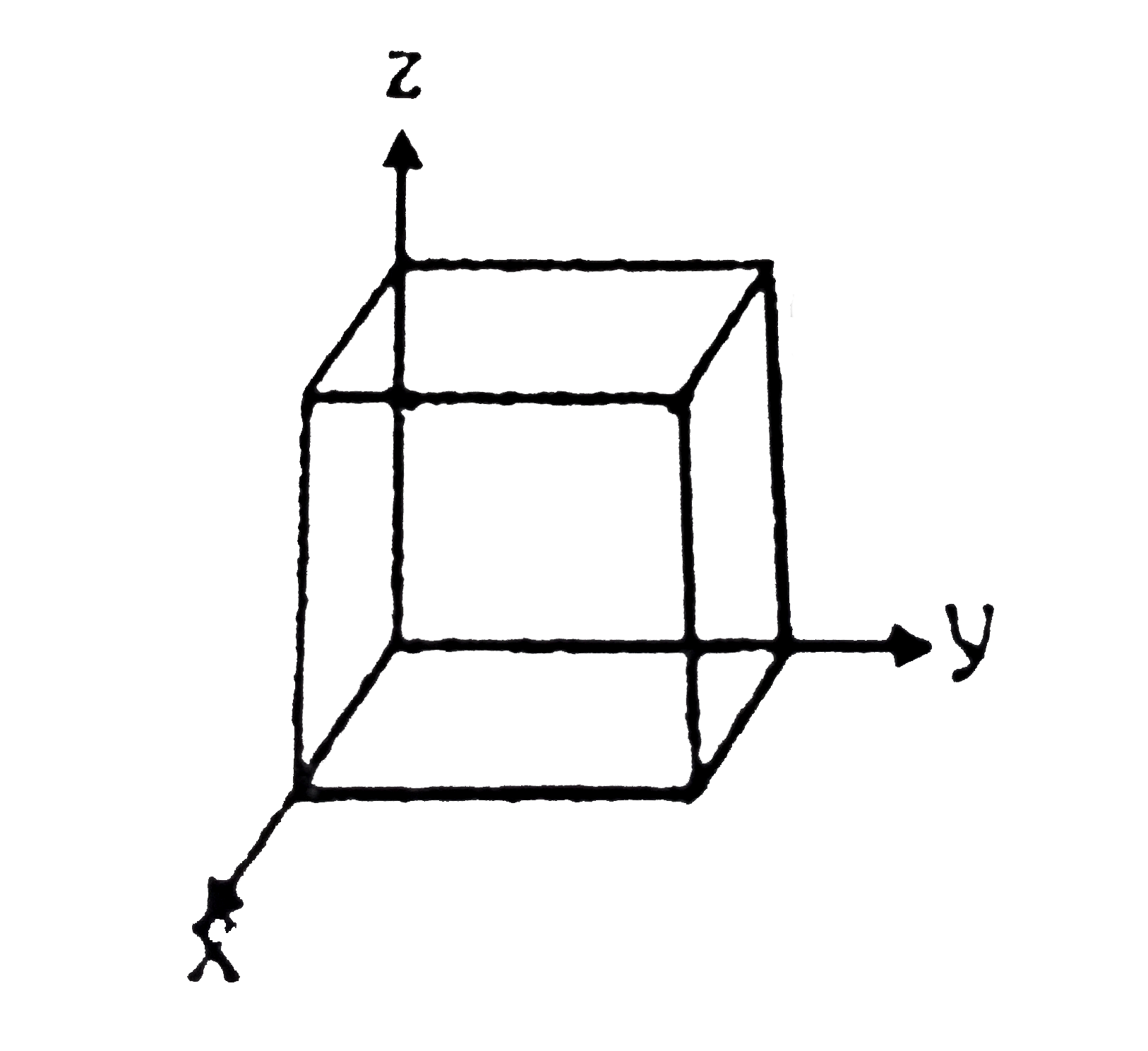
The correct Answer is:2

$ϕ = (6 y) Area - (4 x) Area = 6 \times 1 \times {(1)}^{2} - 4 \times 1 \times {(1)}^{2} = 2$ therefore $\frac{q}{ε_{0}} = 2 \Rightarrow q = 2 ε_{0}$

Updated on:21/07/2023

Class 11 PHYSICS QUESTION BANK

Topper's Solved these Questions

MISCELLANEOUSBOOK - ALLENCHAPTER - MISCELLANEOUSEXERCISE - Part -II Example Some worked out Examples
1 Videos
MISCELLANEOUSBOOK - ALLENCHAPTER - MISCELLANEOUSEXERCISE - Exercise-01
87 Videos
MISCELLANEOUSBOOK - ALLENCHAPTER - MISCELLANEOUSEXERCISE - SUBJECTIVE QUESTION
9 Videos
KINEMATICS (MOTION ALONG A STRAIGHT LINE AND MOTION IN A PLANE)BOOK - ALLENCHAPTER - KINEMATICS (MOTION ALONG A STRAIGHT LINE AND MOTION IN A PLANE)EXERCISE - BEGINNER S BOX-7
8 Videos
PHYSICAL WORLD, UNITS AND DIMENSIONS & ERRORS IN MEASUREMENT BOOK - ALLENCHAPTER - PHYSICAL WORLD, UNITS AND DIMENSIONS & ERRORS IN MEASUREMENT EXERCISE - EXERCISE-IV
8 Videos

Knowledge Check

The electric field in a certain region is given by $\to E = (\frac{K}{x^{3}}) \to i$ . The dimensions of K are -
A $M L T^{- 3} A^{- 1}$
B $M L^{- 2} T^{- 3} A^{- 1}$
C $M L^{4} T^{- 3} A^{- 1}$
Ddimensionless
Electric field is given by $\to E = (8 ˆ i + 4 ˆ j + 3 ˆ k) N C^{- 1}$ . Electric flux through Y-Z plane X-Z plane are in ratio
A $4 : 3 : 8$
B $8 : 4 : 3$
C $3 : 8 : 4$
D $3 : 4 : 8$

The electric potential $V (x)$ in a region around the origin is given by $V (x) = 4 x^{2}$ volts. The electric charge enclosed in a cube of 1 m side with its centre at the origin is (in coulomb
View Solution
Electric field in a region is given by $E = (2 ˆ i + 3 ˆ j - 4 ˆ k) V / m$ . Find the potential difference between points (0, 0, 0) and (1,2,3) in this region.
View Solution
The electric fields in a region is given by $\to E = E_{0} \frac{x}{L} ˆ i$ ,Find the charge contained inside a cubical volume bounded by the surface $x = 0, x = L, y = 0, y = L, z = 0, z = L$ .
View Solution
Electric field function in a region of space is given as → E = y i + x j. The shape of equipotential surface is
View Solution
An electric field is given by $\to E = 4 ˆ i + 3 (y^{2} + 2) ˆ j$ pierces gaussian cube of side 1 m placed at origin such that one of its corners is at origin & rest of sides are along positive side of coordinate axis. If the magnitude of net charge enclosed is n $ɛ_{0}$ then n (in SI units) will be equal to
View Solution
The electric field in a region is given by $\to E = E_{0} \frac{x}{ι} \to i$ . Find the charge contained inside a cubical volume bounded by the curfaced $x = 0, x = α, y = 0, y = α, z = 0 and z = α$ . Take $E_{0} = 5 \times 10^{3} N C^{- 1}$ , $ι = 2 c m and α = 1 c m$ .
View Solution

ALLEN-MISCELLANEOUS-Part -II Example

Two positrons (e+) and two protons (p) are kept on four corners of a s...
03:09
Four charges are placed at the circumference of a dial clock as shown ...
01:12
A small electric dipole is placed at origin with its dipole moment dir...
06:37
Uniform electric field of magnitude 100 V//m in space is directed alon...
08:22
Figure shows a uniformly charged hemisphere of radius R. It has a volu...
04:58
A metallic rod of length I rotates at angular velocity omega about an...
02:39
Consider a finite charged rod. Electric field at point P (shown) makes...
02:20
The alectric potential in a region is given by the relation V(x)=4+5x^...
02:40
A thin homogeneous rod of mass m and length l is free to rotate in ver...
02:52
A thin homogeneous rod of mass m and length l is free to rotate in ver...
02:59
A thin homogeneous rod of mass m and length l is free to rotate in ver...
04:34
A simple pendulum is suspended in a lift which is going up with an acc...
04:35
The variation of potential with distance x from a fixed point is shown...
03:32
The energy density u is plotted against the distance r from the centre...
02:03
The figure shown four situations in which charges as indicated (q gt 0...
03:05
An electric field is given by vec(E)=(yhat(i)+xhat(j))N/C. Find the wo...
02:21
The arrangement shown consists of three elements. (i) A thin rod of ...
03:22
Six charges are kept at the vertices of a regular hexagon as shown in ...
10:42
Electric field in a region is given by vec(E)=-4xhat(i)+6yhat(j). The ...
02:37
An infinite plane of charge with sigma=2 in(0) C/m^(2) is tilted at a ...
03:11

Home
Ask Doubt
Profile

Electric field in a region is given by E → = - 4 x i ^ + 6 y j ^ . The charge enclosed in the cube of side 1 m oriented as shown in the diagram is given by α ∈ 0 . Find the value of α .

The correct Answer is:2

ϕ = ( 6 y ) Area - ( 4 x ) Area = 6 × 1 × ( 1 ) 2 - 4 × 1 × ( 1 ) 2 = 2 therefore q ε 0 = 2 ⇒ q = 2 ε 0

Topper's Solved these Questions

Similar Questions

Knowledge Check

The electric field in a certain region is given by →E=(Kx3)→i. The dimensions of K are -

Electric field is given by →E=(8ˆi+4ˆj+3ˆk)NC−1. Electric flux through Y-Z plane X-Z plane are in ratio

ALLEN-MISCELLANEOUS-Part -II Example

Electric field in a region is given by $\vec{E} = - 4 x \hat{i} + 6 y \hat{j}$ . The charge enclosed in the cube of side $1 m$ oriented as shown in the diagram is given by $α \in_{0}$ . Find the value of $α$ .

$ϕ = (6 y) Area - (4 x) Area = 6 \times 1 \times {(1)}^{2} - 4 \times 1 \times {(1)}^{2} = 2$ therefore $\frac{q}{ε_{0}} = 2 \Rightarrow q = 2 ε_{0}$

The electric field in a certain region is given by $\to E = (\frac{K}{x^{3}}) \to i$ . The dimensions of K are -

Electric field is given by $\to E = (8 ˆ i + 4 ˆ j + 3 ˆ k) N C^{- 1}$ . Electric flux through Y-Z plane X-Z plane are in ratio