A rod of length L and cross section area A has variable density according to the relation ρ(x)=ρ0+kx for 0≤x≤L2 and ρ(x)=2x2 for L2≤x≤L where ρ0 and k are constants. Find the mass of the rod.
The correct Answer is:(7L312+ρ0L2+kL28)A
M1=L/2∫0A(ρ0+kx)dx=(ρ0L2+kL28)A
M2=L∫L/2A(2x2dx)=23[L3−L38]=14L324A
Mtotal=M1+M2=(14L324+ρ0L2+kL28)A
Topper's Solved these Questions
- MISCELLANEOUSBOOK - ALLENCHAPTER - MISCELLANEOUSEXERCISE - EXERCISE-5(A)
15 Videos
- MISCELLANEOUSBOOK - ALLENCHAPTER - MISCELLANEOUSEXERCISE - Exersice -05(B)
20 Videos
- MISCELLANEOUSBOOK - ALLENCHAPTER - MISCELLANEOUSEXERCISE - Exercise-04 [A]
28 Videos
- KINEMATICS (MOTION ALONG A STRAIGHT LINE AND MOTION IN A PLANE)BOOK - ALLENCHAPTER - KINEMATICS (MOTION ALONG A STRAIGHT LINE AND MOTION IN A PLANE)EXERCISE - BEGINNER S BOX-7
8 Videos
- PHYSICAL WORLD, UNITS AND DIMENSIONS & ERRORS IN MEASUREMENT BOOK - ALLENCHAPTER - PHYSICAL WORLD, UNITS AND DIMENSIONS & ERRORS IN MEASUREMENT EXERCISE - EXERCISE-IV
8 Videos
Similar Questions
A thin rod AB of length a has variable mass per unit length ρ0(1+xa) where x is the distance measured from A and ρ0 is a constant.
Find the mass M of the rod.
View SolutionA rod of length L is placed along the x-axis between x=0 and x=L. The linear mass density (mass/length) ρ of the rod varies with the distance x from the origin as ρ=a+bx. Here, a and b are constants. Find the position of centre of mass of this rod.
View Solution
Knowledge Check
If0≤x≤π2then
A2sinx+tanx<3xB2sinx+tanx<2xC2sinx+tanx≤3xD2sinx+tanx≤3xA solid cylindrical wire of length l has cross-section radius a as shown below. The specific resistance of material is given as ρ=ρ0r, where r is distance from axis of cylinder and ρ0 is a positive constant quantity. The resistance across its ends is :
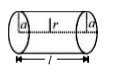 Aρ0l2πaBρ0lπa2Cρ0lπaD2ρ0lπ
Aρ0l2πaBρ0lπa2Cρ0lπaD2ρ0lπThe area of region between y=4−x2,0≤x≤2 and the x-axis is
A43B73C163D53
A thin rod AB of length a has variable mass per unit length P0(1+xa) where x is the distance measured from A and ρ0 is a constant.
Find the position of centre of mass of the rod.
View SolutionA rod of length L is placed along the X-axis between x=0andx=L. The linear density (mass/length) ρ of the rod varies with the distance x from the origin as ρj=a+bx. a. Find the SI units of a and b. b. Find the mass of the rod in terms of a,b, and L.
View SolutionA conductor of uniform area of cross section A has a variable resistivity along its length. What will be the resistance of the conductor if ρ=ρ0(1+αx2), at length l.
View SolutionThe density of a non-uniform rod of length 1 m is given by ρ(x)=a(1+bx2) where a and b are constant and 0≤x≤1.
The centre of mass of the rod will be
View SolutionA liquid of density ρ0 is filled in a wide tank to a height h. A solid rod of length L, cross-section A and density ρ is suspended freely in the tank. The lower end of the rod touches the base of the tank and h=L/n (where n gt 1). Then the angle of inclination θ of the rod with the horizontal in equilibrium position is
View Solution
