Column I shows different charge distributions and short electric dipole at a distance x from the charge distributions. Column II gives the dependence of force acting on the dipole as of function of x.

The correct Answer is:(A) s (B) r (C) p (D) q
(P) Electric field due to uniformly =σ2ε0
Charge thin infinite disc
Fnet on dipole =0
(Q) Electric filed due to uniformaly =σxε0
charged infinite
Fnet on dipole =ρqlε0
(R) Electric field due to uniform =2klx
infinite line of charge
Fnet on.dipole =−2klx(x+l)≈−2kλlx2
(S) Electric field due to uniformly =KQx2
charged sphere
Fnet on dipole =−KQq(2xl)x2(x+l)2≈−KqQ(2xl)x4
≈−2KqQlx3
Topper's Solved these Questions
- MISCELLANEOUSBOOK - ALLENCHAPTER - MISCELLANEOUSEXERCISE - Exercise-07
1 Videos
- MISCELLANEOUSBOOK - ALLENCHAPTER - MISCELLANEOUSEXERCISE - Comprehension 5
5 Videos
- MISCELLANEOUSBOOK - ALLENCHAPTER - MISCELLANEOUSEXERCISE - Exercise-06
1 Videos
- KINEMATICS (MOTION ALONG A STRAIGHT LINE AND MOTION IN A PLANE)BOOK - ALLENCHAPTER - KINEMATICS (MOTION ALONG A STRAIGHT LINE AND MOTION IN A PLANE)EXERCISE - BEGINNER S BOX-7
8 Videos
- PHYSICAL WORLD, UNITS AND DIMENSIONS & ERRORS IN MEASUREMENT BOOK - ALLENCHAPTER - PHYSICAL WORLD, UNITS AND DIMENSIONS & ERRORS IN MEASUREMENT EXERCISE - EXERCISE-IV
8 Videos
Similar Questions
Column-I shows different charge distributions. Cloumn-II gives corresponding electric dipole moments.
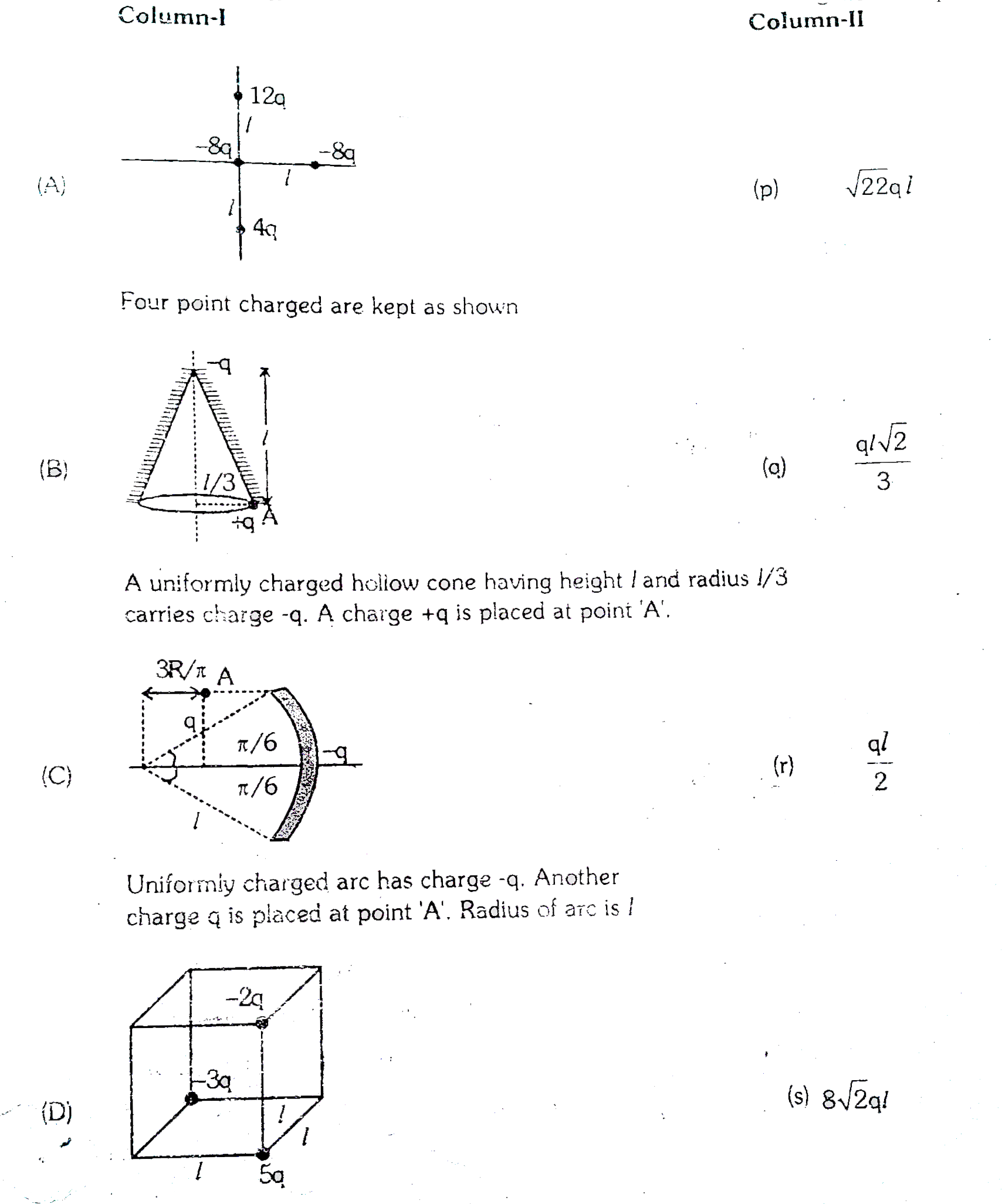
View SolutionThe electric field is measured at a point 0,0, generated due to various charge distributions and the dependence of on is found to be different for different charge distributions. List-I contains different relations between E and . List-II describes different electric charge distributions, along with their locations. Match the functions in List-I with the related charge distributions in List-II.

View Solution
Knowledge Check
The dipole moment of the given charge distribution is
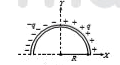 A−4RqπˆiB4RqπˆiC−2RqπˆiD2Rqπˆi
A−4RqπˆiB4RqπˆiC−2RqπˆiD2RqπˆiAs shown in the figure an electric dipole lies at a distance x from the centrr of a chargerd ring of radius R with charge Q uniformly distributed over it .The net force acting on the dipole is
 AaQq4πε0R2−2x22πε0(R2+x2)5/2BaQq2πε0R2+2x22πε0(R2+x2)5/2CaQq4πε0R2+2x22πε0(R2+x2)5/2DaQq2πε0R2−2x22πε0(R2+x2)5/2
AaQq4πε0R2−2x22πε0(R2+x2)5/2BaQq2πε0R2+2x22πε0(R2+x2)5/2CaQq4πε0R2+2x22πε0(R2+x2)5/2DaQq2πε0R2−2x22πε0(R2+x2)5/2Consider the figure given below
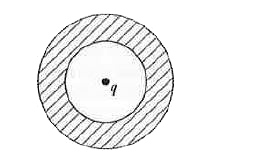
A charge Q is placed inside the Spherical conductor shell. In the given table, column 1 shows different charges, column 2 shows the positions of the electric charge and column 3 shows the different types of charge distribution.

In which case will the charge distribution be non-uniform ?A(I) (i) (M)B(IV) (ii) (M)C(II) (ii) (J)D(I) (iv) (K)
The electric field is measured at a point 0,0, generated due to various charge distributions and the dependence of on is found to be different for different charge distributions. List-I contains different relations between E and . List-II describes different electric charge distributions, along with their locations. Match the functions in List-I with the related charge distributions in List-II.

View SolutionA short electric dipole is placed at a distance x from centre O on the axis of a ring of radius R and charge Q is uniformly distributed over tis.

The net force acting on the dipole will be
View SolutionAn electric dipole is placed in an electric field. Column I is the description of electric field and the angle between the dipole moment →p and the electric field intensity →E and Column II gives the effect of the field on the dipole. Then,

View SolutionConsider the figure given below
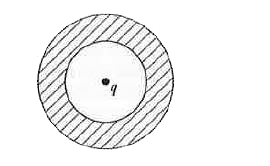
A charge Q is placed inside the Spherical conductor shell. In the given table, column 1 shows different charges, column 2 shows the positions of the electric charge and column 3 shows the different types of charge distribution.

What heppens when the charge is near the conductor shell ?
View SolutionConsider the figure given below
A charge Q is placed inside the Spherical conductor shell. In the given table, column 1 shows different charges, column 2 shows the positions of the electric charge and column 3 shows the different types of charge distribution.

In which case will the Charge distribution be uniform ?
View Solution
