A disc of mass m and radius R lies flat on a smooth horizontal table. A mass less string runs halfway around it as shown in figure. One end of the string is attached to a small body of mass m and the other end is being pulled with a force F. The circumference of the disc is sufficiently rough so that the string does not slip over it. Find acceleration of the small body.
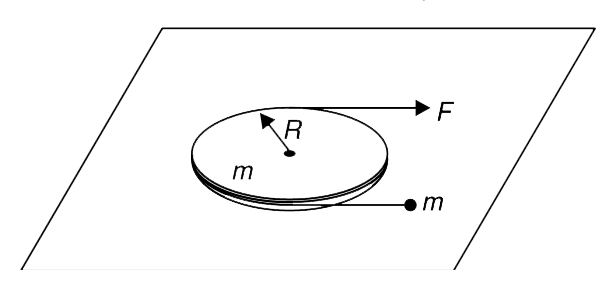
The correct Answer is:a=F4m
Step by step video, text & image solution for A disc of mass m and radius R lies flat on a smooth horizontal table. A mass less string runs halfway around it as shown in figure. One end of the string is attached to a small body of mass m and the other end is being pulled with a force F. The circumference of the disc is sufficiently rough so that the string does not slip over it. Find acceleration of the small body. by Physics experts to help you in doubts & scoring excellent marks in Class 11 exams.
Topper's Solved these Questions
Similar Questions
A disc of mass m lies flat on a smooth horizontal table. A light string runs halfway around it as shown in figure. One end of the string is attached to a particle of mass m and the other end is being pulled with a force F. There is no friction between the disc and the string. Find acceleration of the end of the string to which force is being applied.
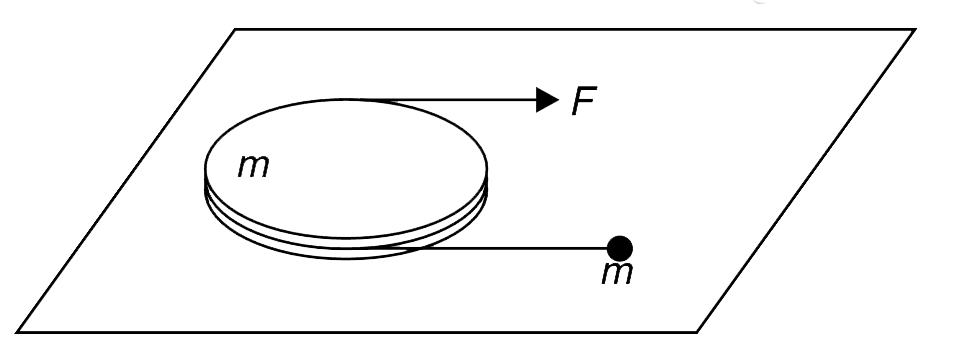 View Solution
View SolutionIn the figure shown a thin light inextensible string is wrapped around a uniform disc. One end of the strin is fixed to the ceiling of the lift and the other end is fied to the circumference of the disc. Acceleration 'a' of the lift is such that the centre of the disc not move with respect to ground. Find the value of ag. String does not slip on pulley.
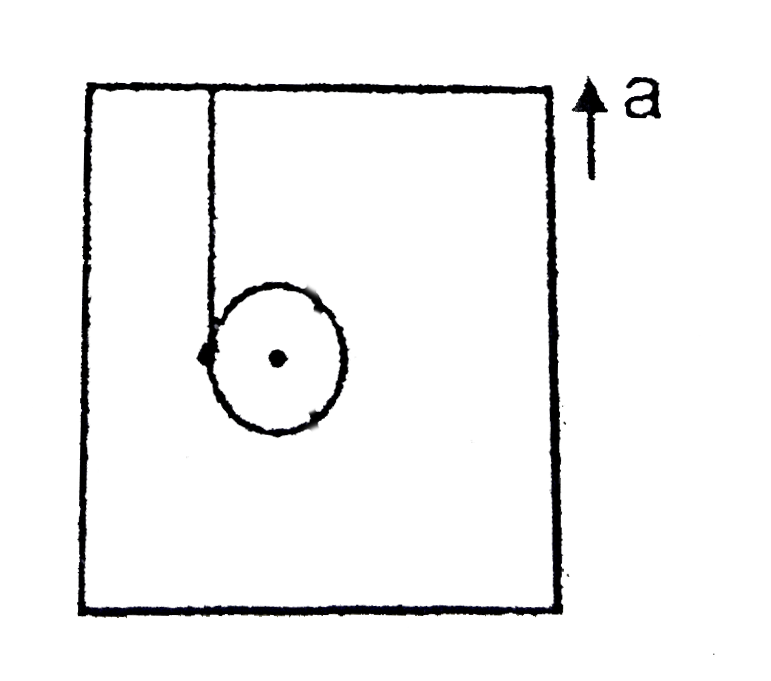 View Solution
View Solution
Knowledge Check
- Question 1 - Select One
In the fig the pulled has a mass M, radius r and the string does not slip over it. The time period of oscillation is
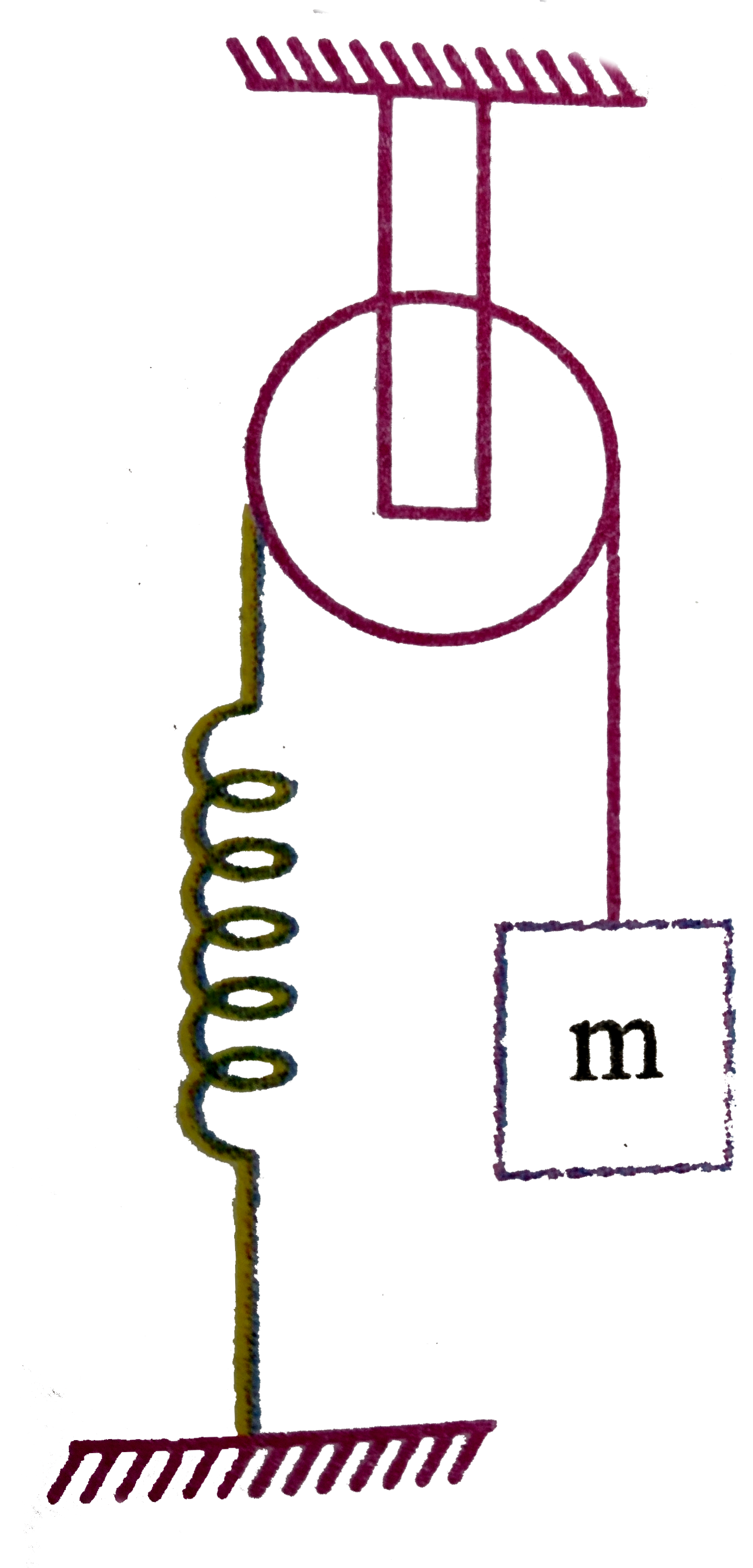 A2π√2m+M2kB2πR√2m+3MR22kC2π√mkD2π√m+Mk
A2π√2m+M2kB2πR√2m+3MR22kC2π√mkD2π√m+Mk - Question 2 - Select One
A block of mass M is pulled on a smooth horizontal table by a string making an angle θ with the horizontal as shown in figure. If the acceleration of the block is a find the force applied by the string and by the table N on the block.
 AT=Matanθ , N=(Mg−Matanθ)BT=Mgcosθ , N=(Mg−Matanθ)CT=Macosθ , N=(Mg−Macosθ)DT=Macosθ , N=(Mg−Matanθ)
AT=Matanθ , N=(Mg−Matanθ)BT=Mgcosθ , N=(Mg−Matanθ)CT=Macosθ , N=(Mg−Macosθ)DT=Macosθ , N=(Mg−Matanθ) - Question 3 - Select One
A block of mass m is attached at the end of an inextensible string which is wound over a rough pulley of mass M and radius R. Assume the string does not slide over the pulley. Find the acceleration of the block when released.
Amg2m+MB2mgm+MCmgm+MD2mg2m+M
A disc of mass m and radius R lies flat on a smooth horizontal table. A particle of mass m, moving horizontally along the table, strikes the disc with velocity V while moving along a line at a distance R2 from the centre. Find the angular velocity acquired by the disc if the particle comes to rest after the impact.
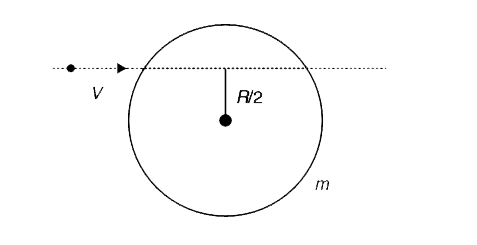 View Solution
View SolutionA disc of mass m and radius r is free to rotate about its centre as shown in the figure. A string is wrapped over its rim and a block of mass m is attached to the free end of the string. The system is released from rest. The speed of the block as it descends through a height h, is :-
 View Solution
View SolutionA unifrom rod of mass m and length L is kept on a horizontal table with L4 length on the table. The end B is tied to a string as shown in the figure. The string attached to the end B is cut and the rod starts rotating about point C. Find the normal reaction from the table on the earth as soon as the string is cut.
 View Solution
View SolutionA uniform disc of radius R and mass M is free to rotate about a fixed horizontal axis perpendicular to its plane and passing through its centre. A string is wrapped over its rim and a block of mass m is attached to the free end of the string. The block is released from rest. If string does not slip on the rim then find the acceleration of the block. Neglect the mass of the string.
View SolutionA uniform disc of mass M and radius R is mounted on a fixed horizontal axis. A block of mass m hangs from a massless string that is wrapped around the rim of the disc. The magnitude of the acceleration of the falling block (m) is
View Solution

