In the last question, the two particles A and B are initially held at a distance r=qQ2π∈0mu2 apart. Particle B is projected directly towards A with velocity u and particle A is released simultaneously. Find the velocity of particle A after a long time. Consider coulomb force only.
The correct Answer is:(1+√32)u
Step by step video, text & image solution for In the last question, the two particles A and B are initially held at a distance r=(qQ)/(2pi in_(0)m u^(2)) apart. Particle B is projected directly towards A with velocity u and particle A is released simultaneously. Find the velocity of particle A after a long time. Consider coulomb force only. by Physics experts to help you in doubts & scoring excellent marks in Class 12 exams.
Updated on:21/07/2023Topper's Solved these Questions
- ELECTROSTATICSBOOK - ARIHANTCHAPTER - ELECTROSTATICSEXERCISE - Level 3
59 Videos
- ELECTROSTATICSBOOK - ARIHANTCHAPTER - ELECTROSTATICSEXERCISE - Level 3
59 Videos
- ELECTROMAGNETIC INDUCTIONBOOK - ARIHANTCHAPTER - ELECTROMAGNETIC INDUCTIONEXERCISE - Level 3
12 Videos
- GEOMETRICAL OPTICSBOOK - ARIHANTCHAPTER - GEOMETRICAL OPTICSEXERCISE - Level 3
9 Videos
Similar Questions
A particle is projected with velocity u at angle θ with horizontal. Find the time when velocity vector is perpendicular to initial velocity vector.
View SolutionA particle moves rectilinearly with initial velocity u and constant acceleration a. Find the average velocity of the particle in a time interval from t=0 to t=t second of its motion.
View Solution
Knowledge Check
A particle is projected in air with an initial velocity u directed at an angle θ above horizontal. After time t0 the velocity of the particle is directed at angle ϕ above horizontal.
AAt time t0 magnitude of verticle component of velocity of the particle is ucosθcotϕBAt time t0 magnitude of rate of change of speed of the particle is gsinϕCThe radius of curvature of the trajectory at time t0 is u2cos2θgcos3ϕDThe value of time t0 is ucosθ(tanθ−tanϕ)/g.The initial velocity given to a particle is u and accelration is given by a=at32 . What will be the velocity of particle after time t.
Au+at52Bu+25at52Cu+52at52Du+at32Two particles A and B are placed as shown in figure. The particle A, on the top of tower, is projected horizontally with a velocity u and particle B is projected along the surface towards the tower, simultaneously. If both particles meet each other, then the speed of projection of particles B is [ignore any friction]
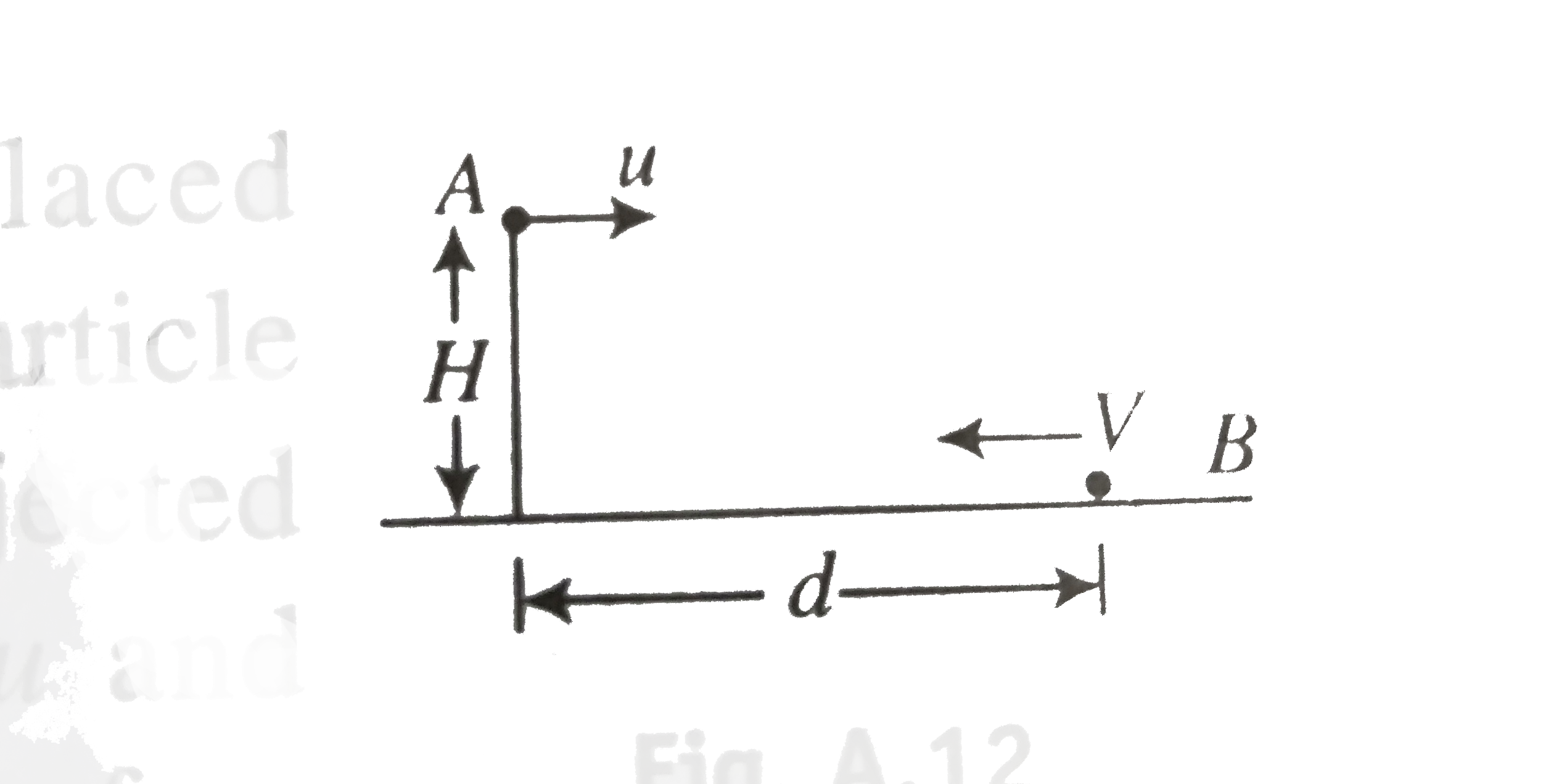 Ad√g2H−uBd√g2HCd√g2H+uDu
Ad√g2H−uBd√g2HCd√g2H+uDu
A particle is projected from ground with velocity 40(√2)m/sat45∘. Find
(a) velocity and
(b) displacement of the particle after 2 s. (g=10m/s2)
View SolutionA particle is thrown with speed u at an angle θ with horizontal.
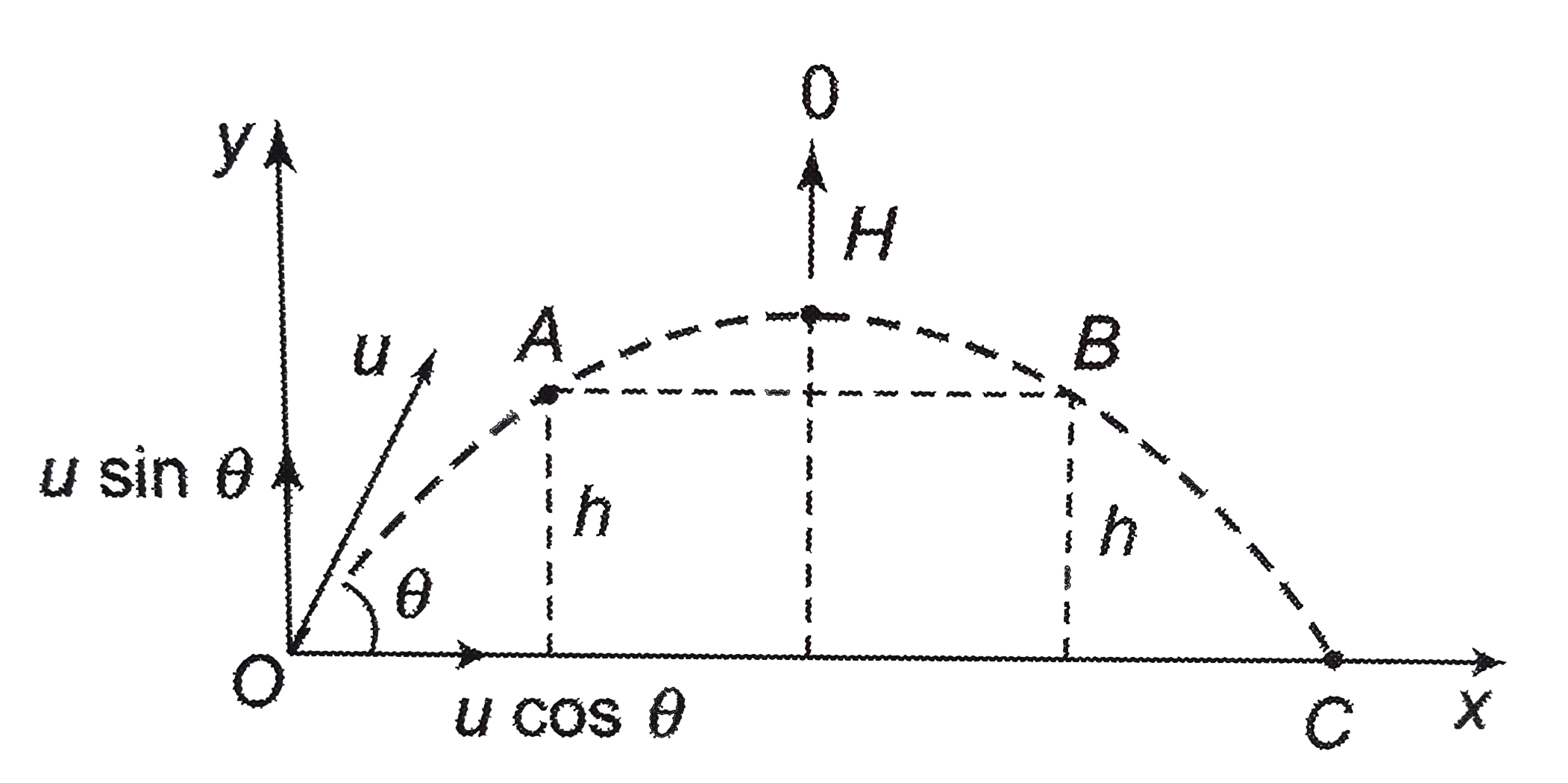
Find the average velocity of particle:
(a) O to C (b) A to B ( c) O to H
View SolutionA particle of mass m is projected with a speed u at an angle θ with the horizontal. Find angular momentum of particle after time t about point of projection.
View SolutionFigure shows that particle A is projected from point P with velocity u along the plane and simultaneously another particle B with velocity v at an angle α with vertical. The particles collide at point Q on the plane. Then
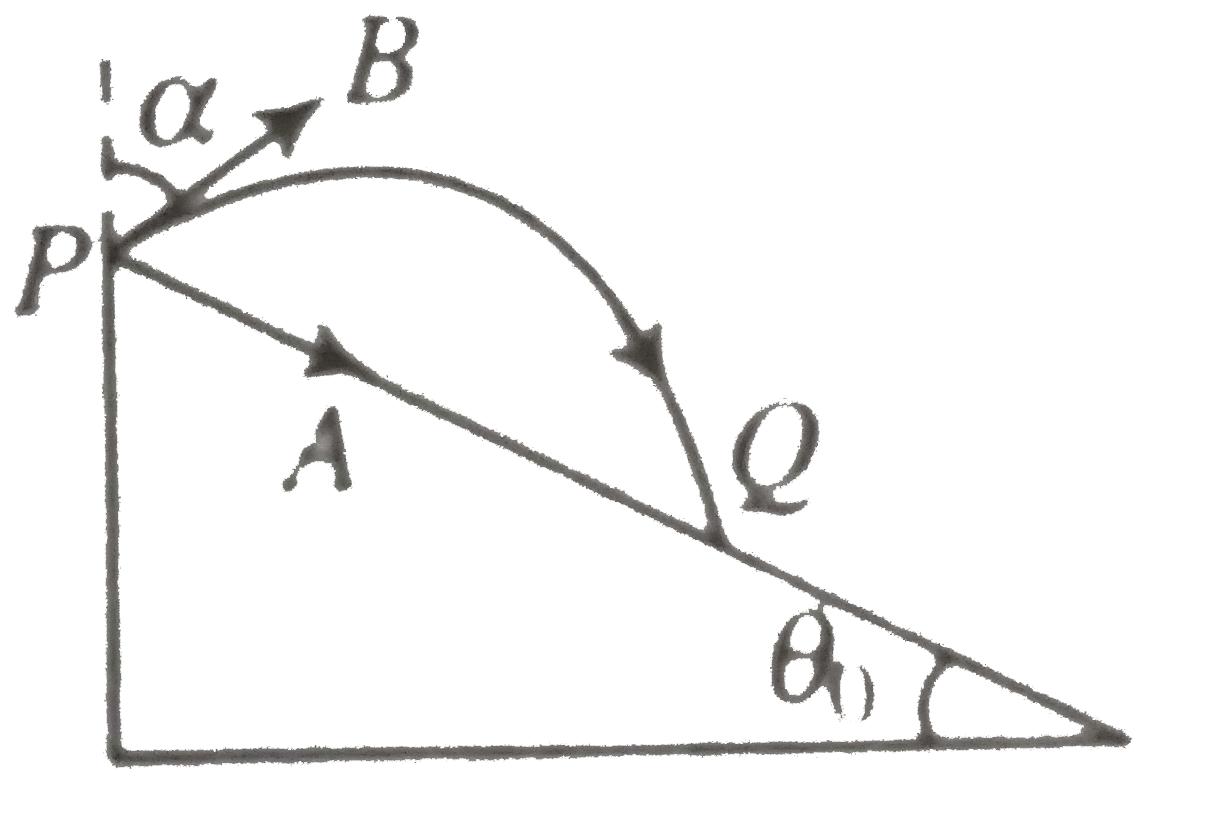
View SolutionA particle is projected from horizontal XZ plane with velocity (uxˆi+uyˆi+uzˆk) from origin (+ yaxis is upward). Find time when velocity of particle will be at 37∘ with horizontal.
View Solution