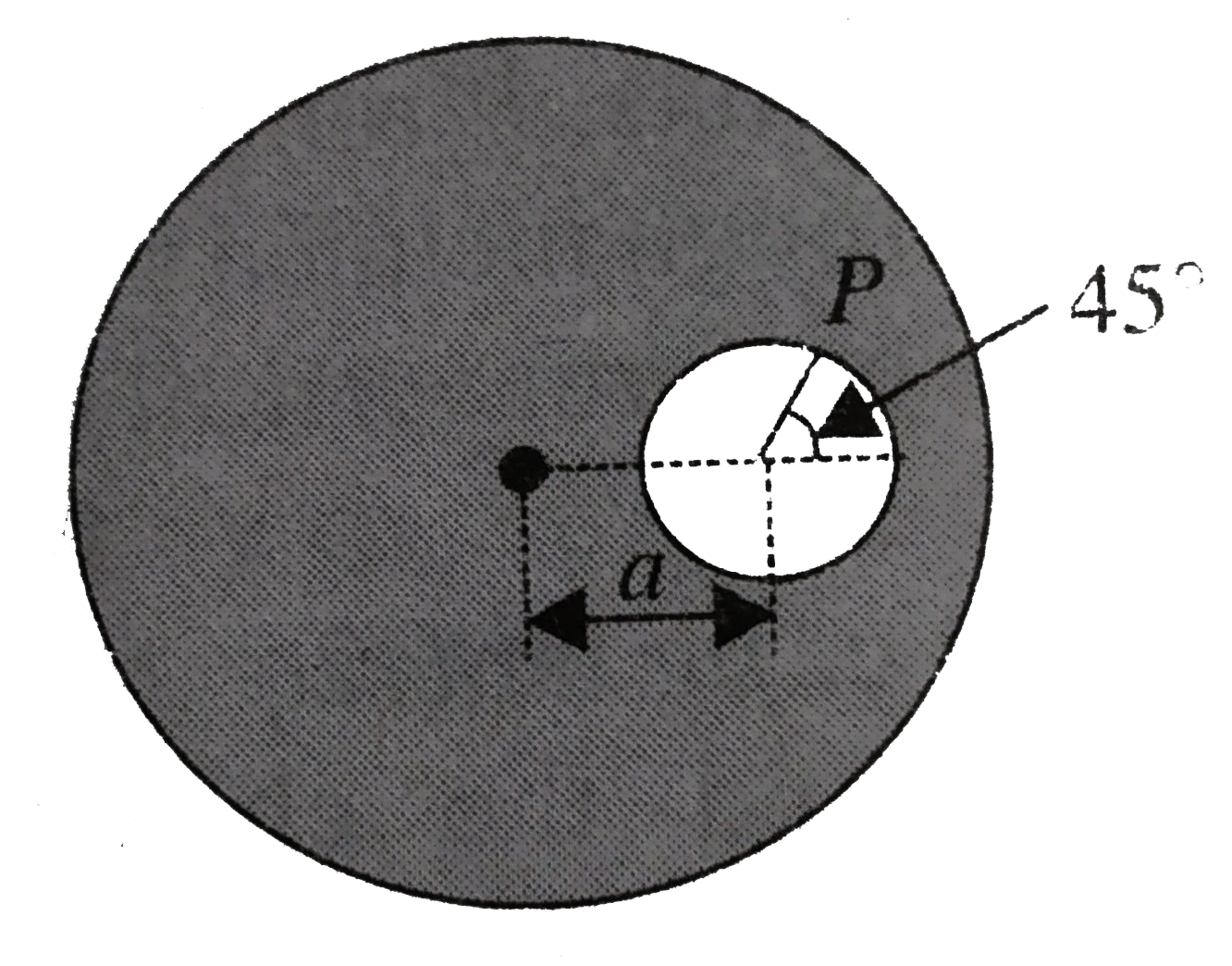
A cavity of radius r is made inside a solid sphere. The volume charge density of the remaining sphere is ρ. An electron (charge e, mass m) is released inside the cavity from point P as shown in figure. The centre of sphere and center of cavity are separated by a distance a. The time after which the electron again touches the sphere is
√6√2rε0mepa
√√2rε0mepa
√6rε0mepa
√rε0mepa
The correct Answer is:B
Torque due to →B = Torque of weight of (QRST) (about QT)
L(B0IL)=3(λL)g(L2+L6)=3λLg(2L3)
B0=2λgI
No external force, so COM cannot displace initial coordinate of COM=3(λL)(zero)+2λL(L2)+λL(L)6λg=L3
Final coordinate of COM=L3(same)
But COM displaces with respect to QT by 2L3. So displacement of QPUT=2L3.
Initial magnetic dipole moment M makes an angle of π4 ACW from +ive x-axis and finally it makes angle 3π4 ACW from +ive x-axis(M=√2IL2)
So change in PE=−MB(cosθ2−cosθ1)=MB0[cos135∘−cos45∘]=2B0IL2=Gain in KE=12Iω2
I(about QT)=2[2λL33+λL3]=10λL33,2B0IL2=12(Iω2)=12(10λL33)ω2,ω2=6B0I5λL
Topper's Solved these Questions
Similar Questions
A cavity of radius r is present inside a solid dielectric sphere of radius R, having a volume charge density of ρ. The distance between the centres of the sphere and the cavity is a. An electron e is kept inside the cavity at an angle θ=45∘ as shown. the electron (mass m and -e) touches the sphere again after time (P√2mrε0eaρ)1/2 ? Find the value of P. Neglect gravity.
 View Solution
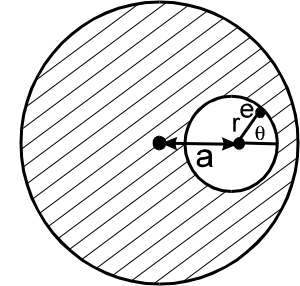
View SolutionA cavity of radius r is present inside a fixed solid dielectric sphere of radius R, having a volume charge density of ρ. The distance between the centres of the sphere and the cavity is a. An electron is released inside the cavity at an angle θ=450 as shown. The electron (of mass m and charge –e) will take (P√2mrε0eaρ)1/2 time to touc the sphere again. Neglect gravity. find the value of P:
 View Solution
View Solution
Knowledge Check
- Question 1 - Select One
A cavity of radius r is made inside a solid sphere. The volume charge density of the remaining sphere is ρ. An electron (charge e, mass m) is released inside the cavity from point P as shown in figure. The centre of sphere and center of cavity are separated by a distance a. The time after which the electron again touches the sphere is
 A√6√2rε0mepaB√√2rε0mepaC√6rε0mepaD√rε0mepa
A√6√2rε0mepaB√√2rε0mepaC√6rε0mepaD√rε0mepa - Question 2 - Select One
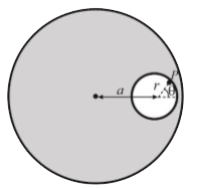
A solid non-conducting sphere of radius R is charged with a uniform volume charge density ρ. Inside the sphere a cavity of radius r is made as shown in the figure. The distance between the centres of the sphere and the cavity is a. An electron of charge 'e' and mass 'm' is kept at point P inside the cavity at angle θ=45∘ as shown. If at t = 0 this electron is released from point P, calculate the time it will take to touch the sphere on inner wall of cavity again.
 A√3Rmε0reρaB√6mε0reρaC√6√3mε0ReρaD√6√2mε0reρa
A√3Rmε0reρaB√6mε0reρaC√6√3mε0ReρaD√6√2mε0reρa - Question 3 - Select One
A positive charge q is placed in a spherical cavity made in a positively charged sphere. The centres of sphere and cavity are displaced by a small distance →l. Force on charge q is :
Ain the direction parallel to vector →lBin radial directionCin a direction which depends on the magnitude of charge density in sphereDdirection can not be determined
A spherical cavity of radius r is made in a conducting sphere of radius 2 r.A charge q is kept at the centre of cavity as shown in the figure.Find the magnitude of the total electric field at (4r 0) .
View SolutionA positive charge q is placed in a spherical cavity made in a positively charged sphere. The centres of sphere and cavity are displaced by a small distance →l. Force on charge q is :
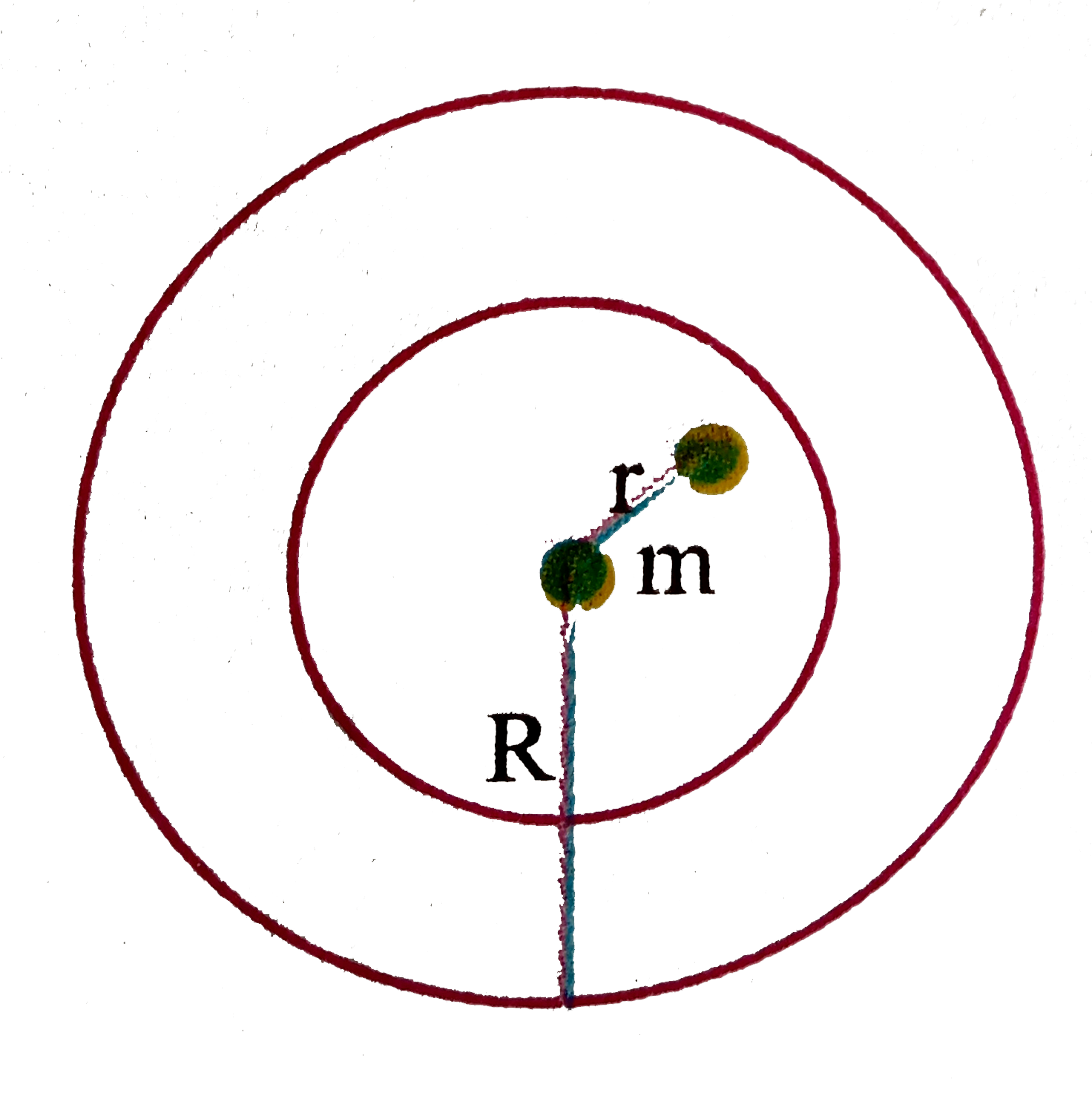
View SolutionA mass m is placed in the cavity inside hollow sphere of mass M as shown in the figure. The gravitational force on m is
 View Solution
View SolutionA hemi-spherical cavity is created in solid sphere (of radius 2R) as shown in the figure. Then
 View Solution
View SolutionA hemispherical cavity of radius R is created in a solid sphere of radius 2R as shown in the figure . Then y -coordinate of the centre of mass of the remaining sphere is
 View Solution
View Solution

