Suppose a,b ∈ R. If the equation x2−(2a+b)x+(2a2+b2−b+1/2)=0 has two real roots, then
A
a=1/2,b=1
B
a=−2,b=−1
C
a=2,b=−1
D
a=−1/2,b=1
Video Solution
Text Solution
The correct Answer is:A
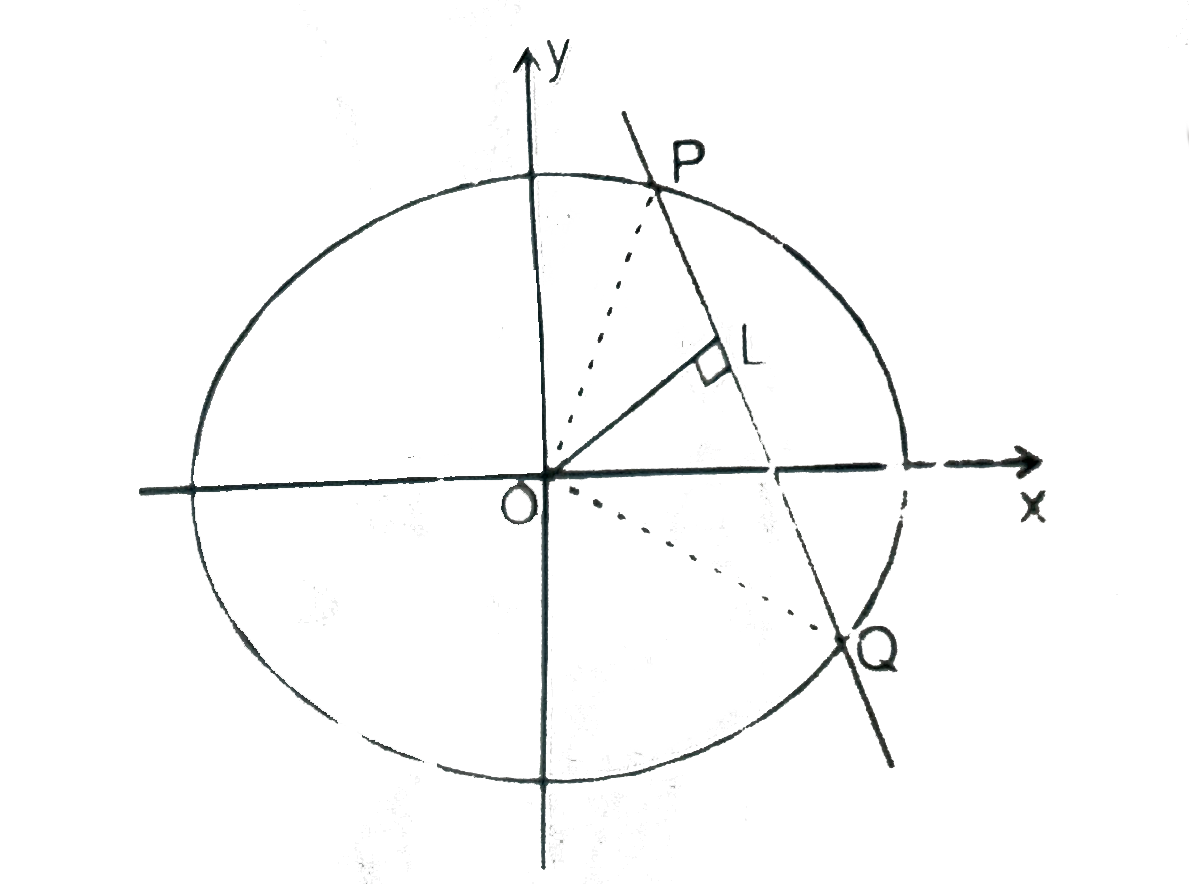
Let L(h, k)
∴Equation of PQ is hx+ky=h2+k2
implies Common equation of pair of lines OP and OQ is
x2a2+y2b2=(hx+kyh2+k2)2 (by homogenized)
∵OP⊥OQ implies Coefficient of x2+ coefficient of y2=0
⇒(1a2+1b2)(h2+k2)=h2+k2
∴ Locus of point L is x2+y2=a2b2a2+b2
|
Updated on:21/07/2023
Topper's Solved these Questions
Similar Questions
Knowledge Check
- Question 1 - Select One
Suppose a, b, c are real numbers, and each of the equations x2+2ax+b2=0 and x2+2bx+c2=0 has two distinct real roots. Then the equation x2+2cx+a2=0 has - (A) Two distinct positive real roots (B) Two equal roots (C) One positive and one negative root (D) No real roots
ATwo distinct positive real rootsBTwo equal rootsCOne positive and one negative rootDNo real roots - Question 2 - Select One
If a,b∈R , and the equation x2+(a−b)x−a−b+1=0 has real roots for all b∈R, then a lies in the in terval
A(1,∞)B(0,∞)C(−∞,1)D(−1,1)
If a,b,c,d∈R, then the equation (x2+ax−3b)(x2−cx+b)(x2−dx+2b)=0 has a. 6 real roots b. at least 2 real roots c. 4 real roots d. none of these
View SolutionIf aandb are positive real numbers and each of the equations x2+3ax+b=0andx2+bx+3a=0 has real roots, then the smallest value of (a+b) is
View SolutionIf a,b∈ R and the equation x2+(a−b)x+1−a−b=0 has unequal roots for all b∈ R then a can be
View SolutionIf aandb are positive numbers and eah of the equations x2+ax+2b=0andx2+2bx+a=0 has real roots, then the smallest possible value of (a+b) is_________.
View SolutionIf the equation x2+a2x+b2=0 has two roots each of which exceeds a number c, then
View SolutionIf a,b,c∈R and the quadratic equation x2+(a+b)x+c=0 has no real roots then
View Solution

