An object is moving in x−y plane its velocity and acceleration at t=0 are represented in figure.

The ratio of magnitude of velocity to magnitude of component of acceleration along velocity at t=0 :-
83
85
2
58
The correct Answer is:C
v5cos37∘=84=2
Topper's Solved these Questions
- TEST PAPERBOOK - ALLENCHAPTER - TEST PAPEREXERCISE - Exercise (Physics)
330 Videos
- TEST PAPERBOOK - ALLENCHAPTER - TEST PAPEREXERCISE - PHYSICS
4 Videos
- SIMPLE HARMONIC MOTIONBOOK - ALLENCHAPTER - SIMPLE HARMONIC MOTIONEXERCISE - Example
1 Videos
- TEST PAPER 1BOOK - ALLENCHAPTER - TEST PAPER 1EXERCISE - PHYSICS
11 Videos
Similar Questions
A particle moves in such a way that its position vector at any time tist "is" hati+12t2ˆj+tˆK Find a function of time (a) the velocity, (b) the speed, (c) the acceleration, (d) the magnitude of the acceleration, (e) the magnitude of the component of acceleration along velocity (called tangential' acceleration), (f) the magnitude of the component ofacceleration perpendicular to velocity (called normal acceleration).
View SolutionA particle moves in such a way that its position vector at any time t is →r=tˆi+12t2ˆj+tˆk.
Find as a function of time:
(i) The velocity (d→rdt) (ii) The speed (∣∣∣d→rdt∣∣∣) (iii) The acceleration (d→vdt)
(iv) The magnitude of the acceleration
(v) The magnitude of the component of acceleration along velocity (called tangential acceleration)
(v) The magnitude of the component of acceleration perpendicular to velocity (called normal acceleration).
View Solution
Knowledge Check
An object is moving in x−y plane its velocity and acceleration at t=0 are represented in figure.

After how much time object crosses the y−axis:-A4secB2secC3secDNoneIn (Q. 24.) the tension in string is T and the linear mass density of string is μ. The ratio of magnitude of maximum velocity of particle and the magnitude of maximum acceleration is
A12π√μl2TB2π√μl2TC12π√Tμl2D14π√μl2TThe velocity-time graph of a body is shown in figure. The ratio of magnitude of average acceleration during the intervals OA and AB is
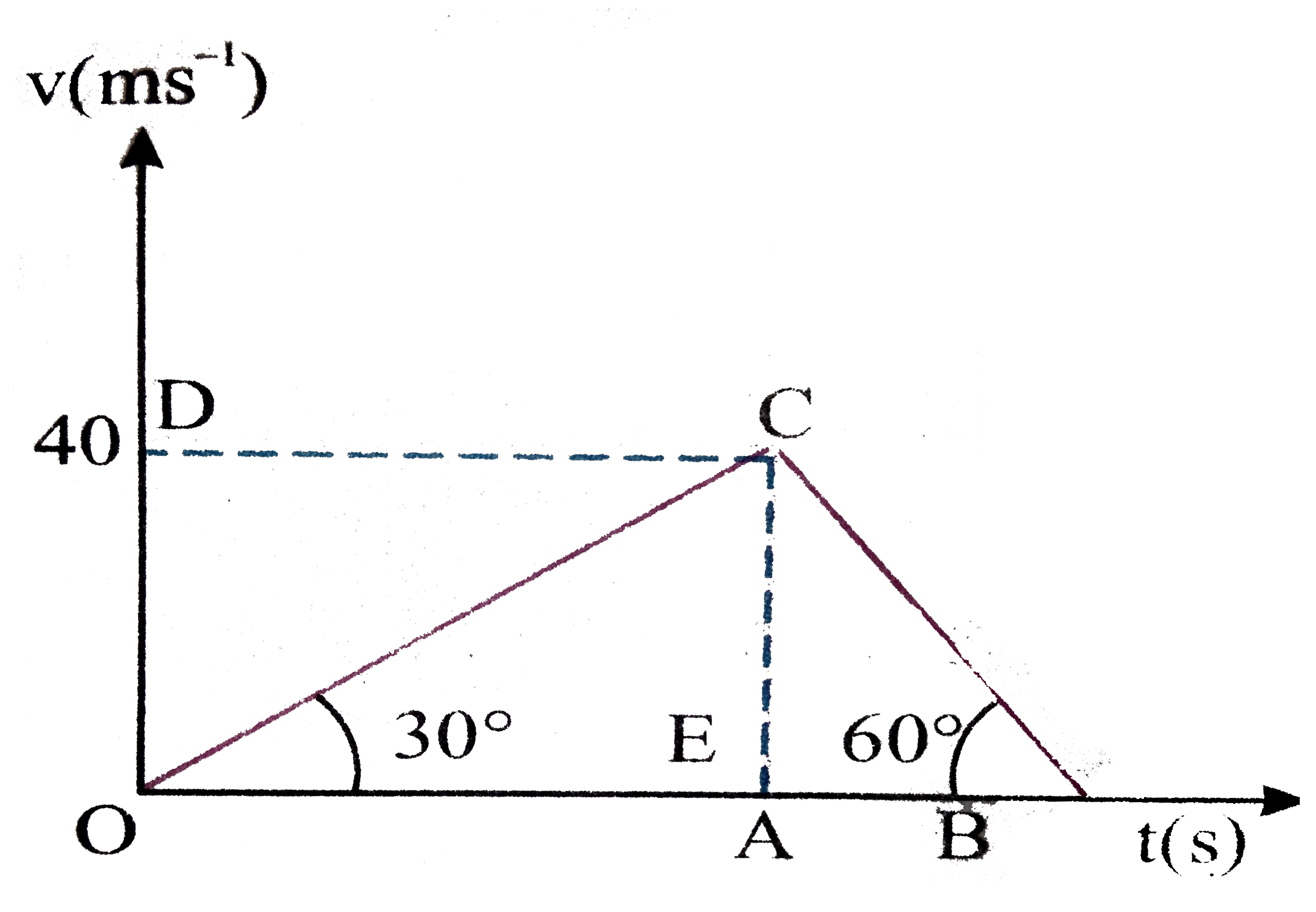 A1B12C13D3
A1B12C13D3
A particle moves in the x-y plane with the velocity ¯v=aˆi−btˆj. At the instant t=a√3/b the magnitude of tangential, normal and total acceleration are _&_.
View Solution
A particle is moving in x–y plane. The x and y components of its acceleration change with time according to the graphs given in figure. At time t=0, its velocity is v0 directed along positive y direction. if a0=v0t0, find the angle that the velocity of the particle makes with x axis at time t=4t0.
View SolutionA body moves with constant angular velocity on a circle. Magnitude of angular acceleration
View SolutionFor the acceleration - time (a - t) graph shown in figure, the change in velocity of particle from t = 0 to t = 6 s is
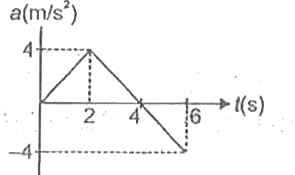
View SolutionA particle is moving eastwards with a velocity 5ms−1, changes its direction northwards in 10 seconds and moves with same magnitude of velocity. The average acceleration is
View Solution
