The compenent of →A=ˆi+ˆj+5ˆj perpendicular to →B=3ˆi+4ˆj is
−425ˆi+325ˆj+5ˆk
−825ˆi−625ˆj+5ˆk
425ˆi−325ˆj+5ˆk
+825ˆi−625ˆj+5ˆk
The correct Answer is:C
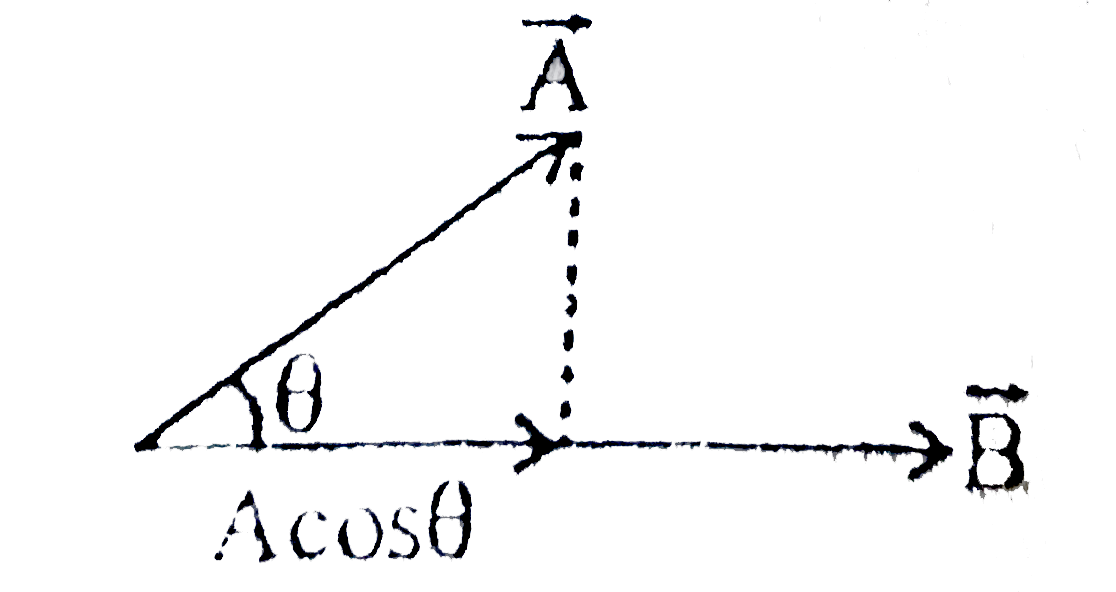
→A11=Acosθ=A(→A.→BAB)=→A.→BA=3+45=75
→A11=75(3ˆi+4ˆj5)=725(3ˆi+4ˆj)
→A11=2125ˆi+2825ˆj
→A⊥=(ˆi+ˆj+5ˆk)−(2125ˆi+2825ˆj)
425ˆi−325ˆj+5ˆk
Topper's Solved these Questions
- TEST PAPERBOOK - ALLENCHAPTER - TEST PAPEREXERCISE - PHYSICS
4 Videos
- TEST PAPERBOOK - ALLENCHAPTER - TEST PAPEREXERCISE - PHYSICS
4 Videos
- SIMPLE HARMONIC MOTIONBOOK - ALLENCHAPTER - SIMPLE HARMONIC MOTIONEXERCISE - Example
1 Videos
- TEST PAPER 1BOOK - ALLENCHAPTER - TEST PAPER 1EXERCISE - PHYSICS
11 Videos
Similar Questions
Component of →a=ˆi−ˆj−ˆk perpendicular to thevector →b=2ˆi+ˆj−ˆk is
View SolutionFind the area of the parallelogram whose adjacent sides are represented by the vectors (i) →a=ˆi+2ˆj+3ˆk and →b=−3ˆi−2ˆj+ˆk (ii) →a=(3ˆi+ˆj+4ˆk) and →b=(ˆi−ˆj+ˆk) (iii) →a=2ˆi+ˆj+3ˆkand→b=ˆi−ˆj (iv)→b=2ˆiand→b=3ˆj.
View Solution
Knowledge Check
If →A=−2ˆi+3ˆj−4ˆkand→B=3ˆi−4ˆj+5ˆk then →A×→B is
Aˆi−2ˆj−ˆkB−ˆi+2ˆj−ˆkC−ˆi−2ˆj+ˆkD−ˆi−2ˆj−ˆkThree vectors →A=2ˆi−ˆj+ˆk,→B=ˆi−3ˆj−5ˆk, and →C=3ˆi−4ˆj−4ˆk are sides of an :
Aequilateral triangleBright angled triangleCisosceles triangleDnone of theseIf →A and →B are perpendicular Vectors and vector →A=5ˆi+7ˆj−3ˆk and →B=2ˆi+2ˆj−aˆk. The value of a is
A-2B8C7D-8
Find →a.→b when
(i) →a=ˆi−2ˆj+ˆk and →b=3ˆi−4ˆj−2ˆk
(ii) →a=ˆi+2ˆj+3ˆk and →b=−2ˆj+4ˆk
(iii) →a=ˆi−ˆj+5ˆk and →b=3ˆi−2ˆk
View Solutiona. Prove that the vector →A=3ˆi−2ˆj+ˆk, →B=ˆi−3ˆj+5ˆk, and →C=2ˆi+ˆj−4ˆk from a right -angled triangle.
b. Determine the unit vector parallel to the cross product of vector →A=3ˆi−5ˆj+10ˆk & =→B=6ˆi+5ˆj+2ˆk.
View SolutionFind the angle between the vectors →a and →b, when
(i) →a=ˆi−2ˆj+3ˆk and →b=3ˆi−2ˆj+ˆk
(ii) →a=3ˆi+ˆj+2ˆk and →b=2ˆi−2ˆj+4ˆk
(iii) →a=ˆi−ˆj and →b=ˆj+ˆk.
View SolutionIf →a=2ˆi+2ˆj+ˆk,→b=−ˆi+ˆj+2ˆk and →c=3ˆi+ˆj such that →a+λˆ(b) is perpendicular to→c , find λ.
View SolutionFind (→a×→b) and ∣∣→a×→b∣∣,when
(i) →a=ˆi−ˆj+2ˆk and →b=2ˆi+3ˆj−4ˆk
(ii)→a=2ˆi+ˆj+3ˆk and →b=3ˆi+5ˆj−2ˆk
(iii) →a=ˆi−7ˆj+7ˆk and →b=3ˆi−2ˆj+2ˆk
(iv) →a=4ˆi+ˆj−2ˆk and →b=3ˆi+ˆk
(v) →a=3ˆi+4ˆj and →b=ˆi+ˆj+ˆk
View Solution
