A constant force produces maximum velocity V on the block connected to the spring of force constant K as shown in the fig. When the force constant of spring becomes 4K the maximum velocity of the block is

V4
2V
V2
V
The correct Answer is:C
At maximum, velocity, Fnet=0⇒F=kx
By work energy theorem, W=ΔKE
Fx−12Kx2=12mV2−0
⇒F22K=12mV2⇒V∝1√K
Topper's Solved these Questions
Similar Questions
A spring of force constant k is cut into 4 equal parts. The spring constant of each piece become …….. times and time period will become ……times.
View SolutionTwo blocks A and B of mass 2m and m respectively are connected to a massless spring of force constant K as shown in figure A and B are moving on the horizontal frcitionless surface with velocity v to right with underformed spring. If B collides with C elastically, then maximum compression of the spring will be
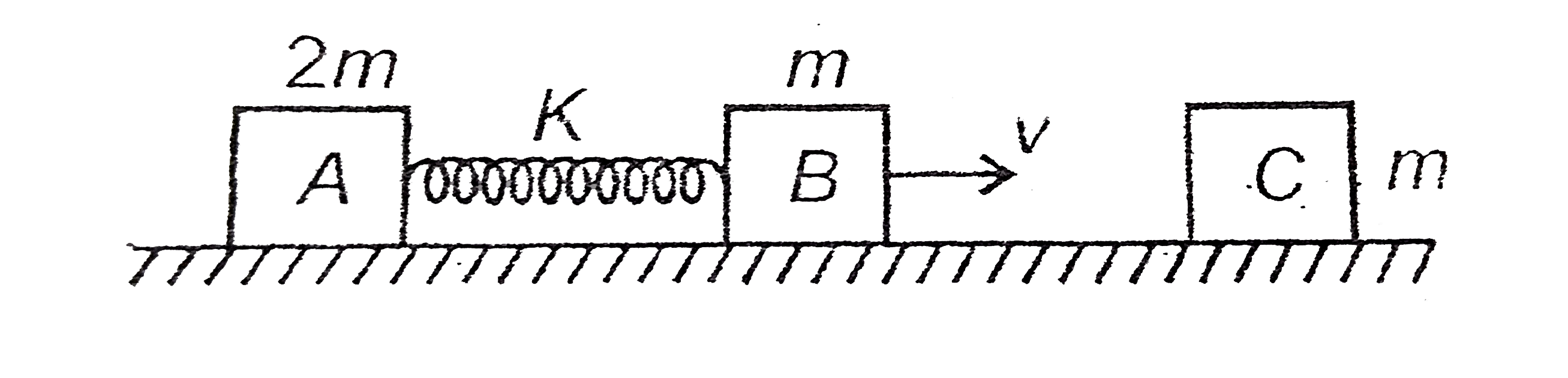 View Solution
View Solution
Knowledge Check
- Question 1 - Select One
A constant force produces maximum velocity V on the block connected to the spring of force constant K as shown in the figure. When the force constant of spring becomes 4K, the maximum velocity of the block is
 AV/4B2VCV/2DV
AV/4B2VCV/2DV - Question 2 - Select One
One-forth length of a spring of force constant K is cut away. The force constant of the remaining spring will be
A34KB43KCKD4 K - Question 3 - Select One
Force constant of a spring (k) is anonymous to
AYALBYLACALYDALY
A block of mass m is suspended by different springs of force constant shown in figure.
 View Solution
View SolutionAn ideal spring of force constant k is broken into two identical pieces. The force constant of each of the smaller springs is :
View SolutionAn ideal spring of force constant k is broken into two identical pieces. The force constant of each of the smaller springs is :
View SolutionTwo springs of force constant k and 2k are connected to a mass shown in figure the frequency of oscillation of the mass is
 View Solution
View SolutionTwo springs of force constant k and 2k are connected to a mass shown in figure the frequency of oscillation of the mass is
 View Solution
View Solution

