Find the value of $x_{1}$ , so that $\int_{0}^{x_{1}} y d x = 5$

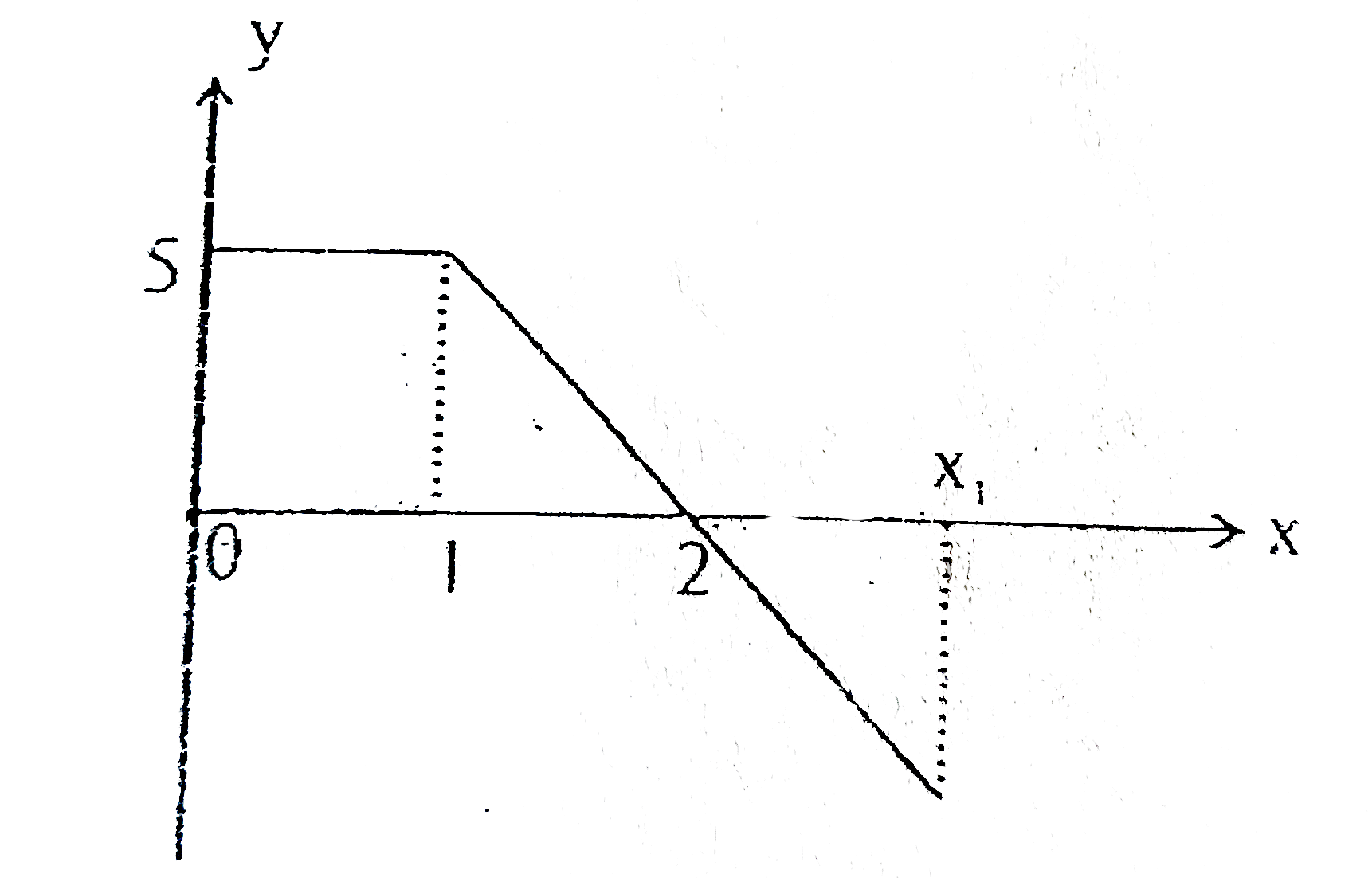
A

$5$

B

$3$

C

$2$

D

$1$

Video Solution

Text Solution

Verified by Experts

The correct Answer is:B

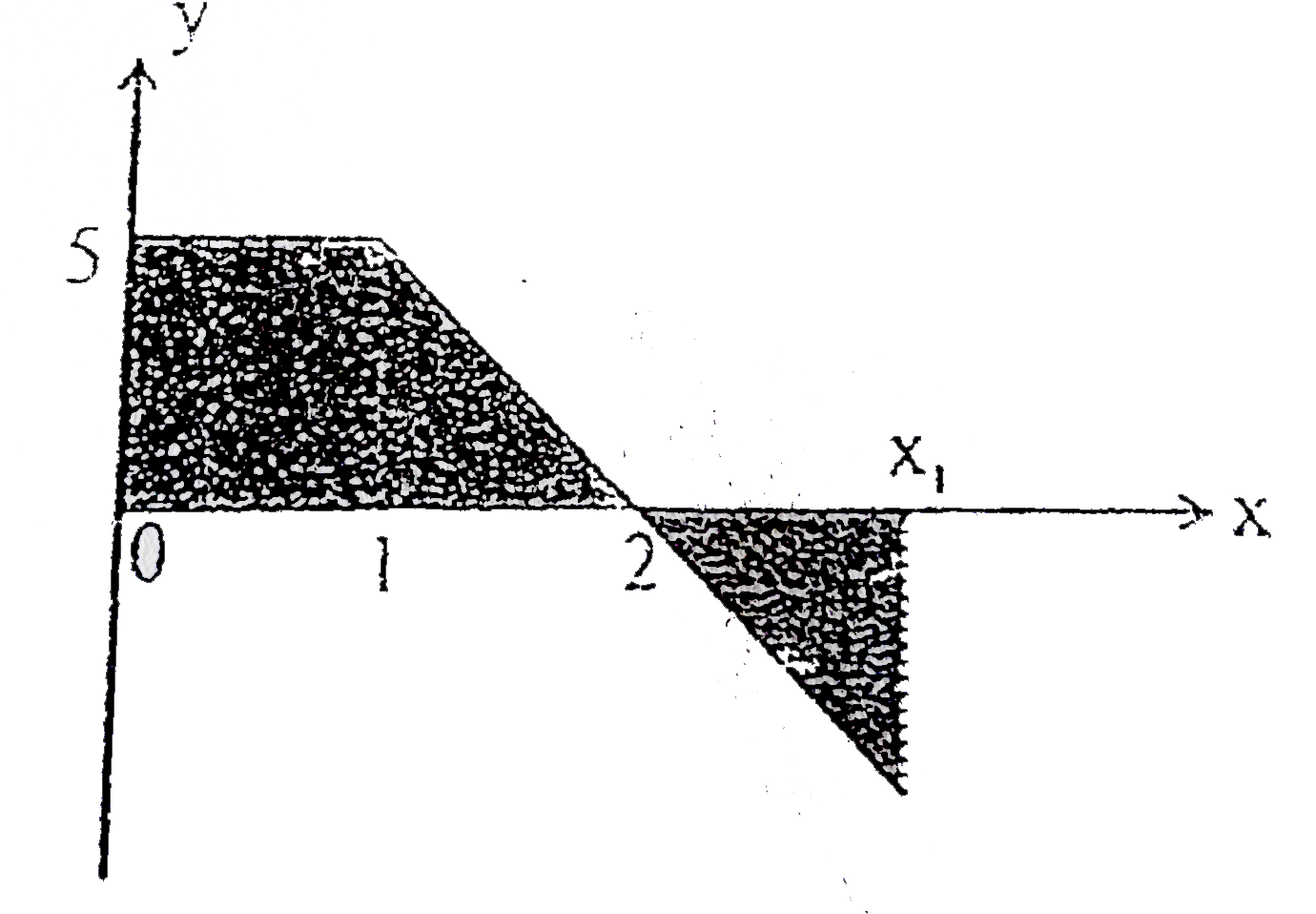
$\int_{0}^{x_{1}} y d x =$ shadded area
$(5 \times 1) + \frac{1}{2} \times (1 + 5) - \frac{1}{2} \times (x_{1} - 2) \times 5 (x_{1} - 2)$
$x_{1} = 3$

|

Updated on:21/07/2023

Class 12 PHYSICS TEST PAPER

Topper's Solved these Questions

Similar Questions

Knowledge Check

Question 1 - Select One
The value of the integral $\int_{0}^{1} x {(1 - x)}^{n} d x$ , is
A $\frac{1}{n + 1} + \frac{1}{n + 2}$
B $\frac{1}{(n + 1) (n + 2)}$
C $\frac{1}{n + 2} - \frac{1}{n + 1}$
D $2 (\frac{1}{n + 1} - \frac{1}{n + 2})$
Question 2 - Select One
The value of the integral $\int_{0}^{1} x {(1 - x)}^{n} d x$ is
A $\frac{1}{n + 1} + \frac{1}{n + 2}$
B $\frac{1}{(n + 1) (n + 2)}$
C $\frac{1}{n + 2} - \frac{1}{n + 1}$
D $2 (\frac{1}{n + 1} - \frac{1}{n + 2})$

ALLEN-TEST PAPER-Exercise (Physics)

Home
Ask Doubt
Profile