The following curve represents a function y=f(x). Find average value of y when x changes from 0 to 6

(20)/(3)
(25)/(3)
(35)/(3)
(40)/(3)
The correct Answer is:B
→y=∫60ydx6=253
Topper's Solved these Questions
- TEST PAPERBOOK - ALLENCHAPTER - TEST PAPEREXERCISE - PHYSICS
4 Videos
- TEST PAPERBOOK - ALLENCHAPTER - TEST PAPEREXERCISE - PHYSICS
4 Videos
- SIMPLE HARMONIC MOTIONBOOK - ALLENCHAPTER - SIMPLE HARMONIC MOTIONEXERCISE - Example
1 Videos
- TEST PAPER 1BOOK - ALLENCHAPTER - TEST PAPER 1EXERCISE - PHYSICS
11 Videos
Similar Questions
Knowledge Check
The following curve represent rate of change of a variable y w.r.t. x. The change in the value of y when x changes from 0 to 11 is:
 A60B25C35D85
A60B25C35D85The following curve represent rate of change of a variable y w.r.t. x. The charge in the value of y when x changes from 0 to 11 is :
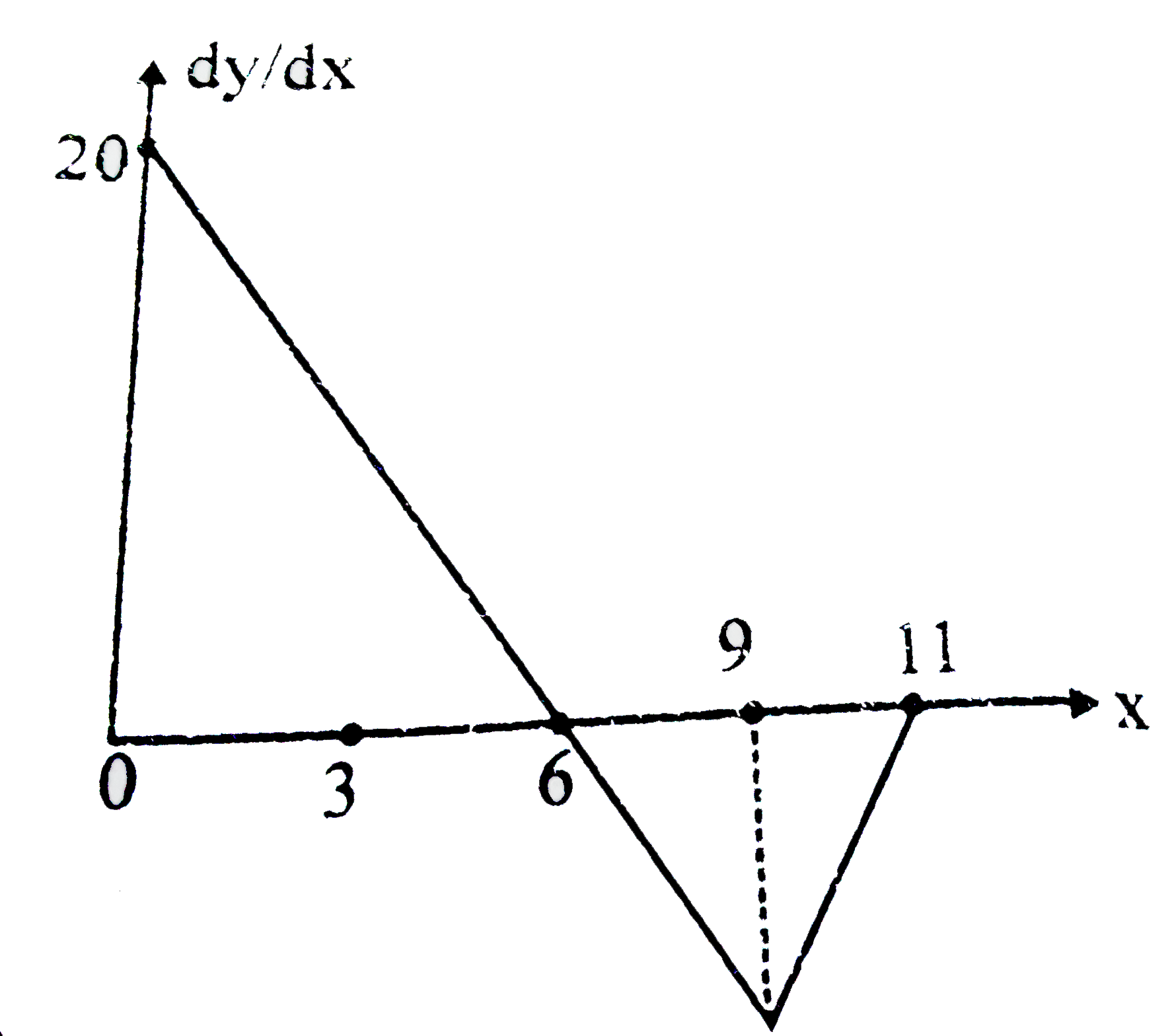 A60B25C35D85
A60B25C35D85If f(x) is an even function, then the curve y=f(x) is symmetric about
Ax-axisBy-axisCboth the axesDnone of these
A function f(x) satisfies the following property: f(x.y)=f(x)f(y). Show that the function f(x) is continuous for all values of x if it is continuous at x=1.
View SolutionCheck whether the followings represent function or not (i) x2+y2=36,y∈[0,6]
View SolutionLet f(x)=[x]+1{x}+1 for f:[0,52)→(12,3], where [⋅] represents the greatest integer function and {⋅} represents the fractional part of x.
Draw the graph of y=f(x). Prove that y=f(x) is bijective. Also find the range of the function.
View SolutionA function f:R→R satisfies the equation f(x+y)=f(x)f(y) for all values of x and y and for any x∈R,f(x)≠0. Suppose the function is differentiable at x=0 and f'(0)=2, then for all x∈R,f(x)=
View SolutionA function f:R→R satisfies the equation f(x+y)=f(x)f(y) for all values of x and y and for any x∈R,f(x)≠0. Suppose the function is differentiable at x=0 and f' (0) = 2, then for all x∈R,f(x)=
View Solution
