A stone is thrown at a speed of $20 m / s$ from top of a building of height 25 m. Find out how far from the foot of building can the stone be thrown.

Video Solution

Text Solution

Verified by Experts

This can be maximizing x varying $θ$ on ground.

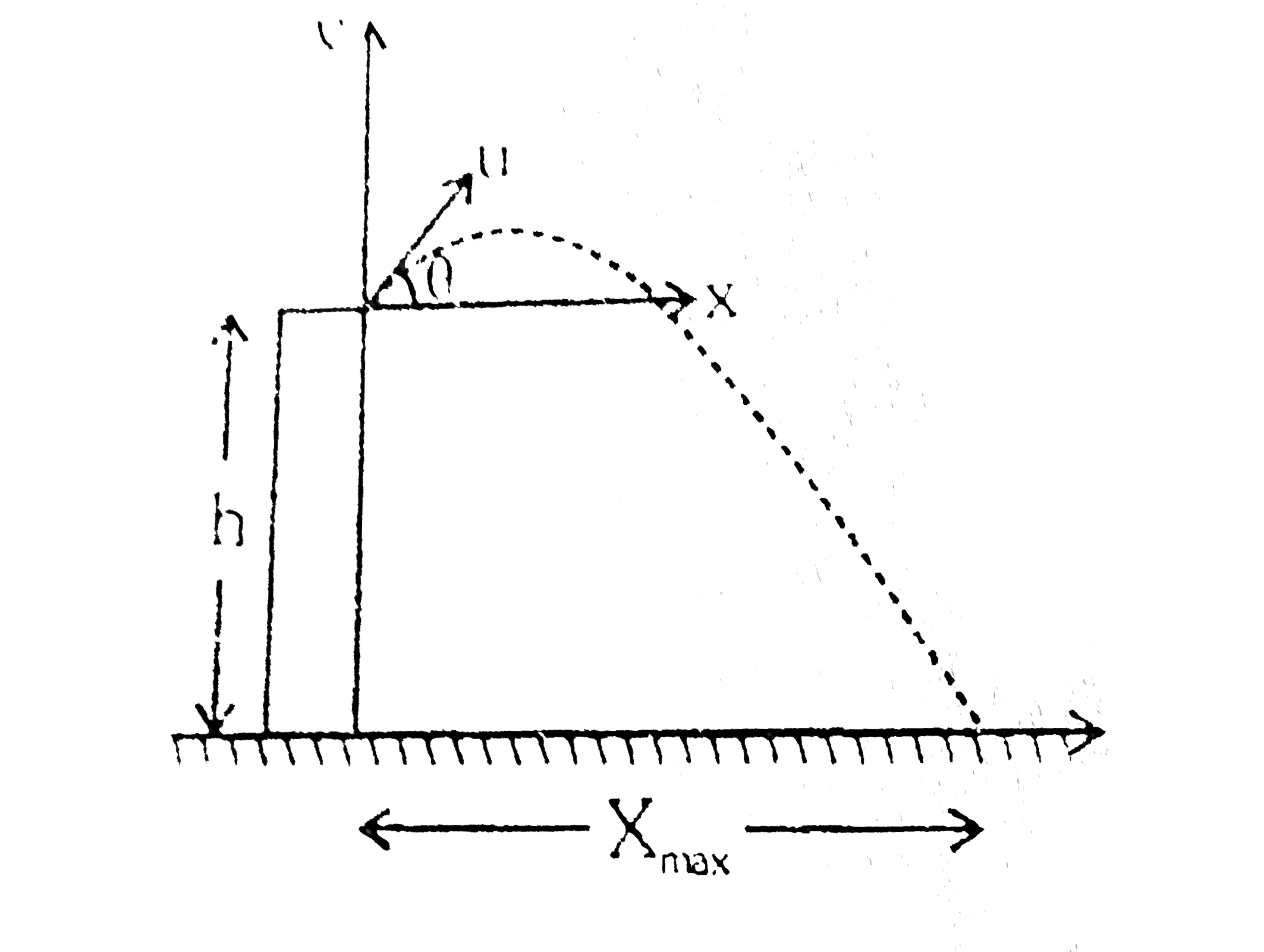
By $y = x tan θ - \frac{g x^{2} (1 + {tan}^{2} θ)}{2 u^{2}}$
$- 25 = x tan θ - \frac{10 x^{2} (1 + {tan}^{2} θ)}{2 \times 400}$
${tan}^{2} θ (x^{2}) - tan (80 x) + (x^{2} - 2000) = 0$
It is quadratic in $tan θ$ & for $tan θ$ to be real
$6400 x^{2} - 4 x^{2} (x^{2} - 2000) > 0$
$x_{max} = 60 m$

|

Updated on:21/07/2023

Class 11 PHYSICS RECTILINEAR MOTION

Topper's Solved these Questions

Similar Questions

Knowledge Check

Question 1 - Select One
A ball is thrown horizontally with a speed of $20 m / s$ from the top of a tower of height 100m
Time taken by the ball to strike the ground is
A $\sqrt{20} s$
B $2 \sqrt{20} s$
C $4 \sqrt{20} s$
D $10 s$
Question 2 - Select One
A stone dropped from a building of height $h$ and it reaches after $t$ second on the earth. From the same building if two stones are thrown (one upwards and other downwards) with the same speed and they reach the earth surface after $t_{1}$ and $t_{2}$ seconds, respectively, then
A $t = t_{1} - t_{2}$
B $t = \frac{t_{1} + t_{2}}{2}$
C $t = \sqrt{t_{1} t_{2}}$
D $t = t_{1}^{2} t_{2}^{2}$
Question 3 - Select One
A ball is thrown horizontally with a speed of $20 m / s$ from the top of a tower of height 100m
velocity with which the ball strikes the ground is .
A $20 \sqrt{6} m / s$ at angle ${tan}^{- 10 (\sqrt{7})}$ below the horizontal
B $20 \sqrt{6} m / s$ at an angle ${tan}^{- 1} (\sqrt{6})$ below the horizontal
C $20 \sqrt{6} m / s$ at an angle ${tan}^{- 1} (\sqrt{5})$ below the horizontal
D $10 \sqrt{6} m / s$ at an angle ${tan}^{- 1} (\sqrt{5})$ below the horizontal

ALLEN-KINEMATICS-Integer Type Question

Home
Ask Doubt
Profile