If two particle are projected as shown then find i.e.,

(i) Particle collide or not.
(ii) If collide, then find collision time
tanθ=1010√3=1√3
θ=30∘
θ=tan−1=(uAByuABx)=tan−1(5√315)=30∘
Here uABy=uAy−uBy=0−(−10sin60∘)=5√3m/s
uABx=uAx−uBx=10−(−10cos60∘)=15m/s
So uAB is along AB particle will collide.
uAB=√152+(5√3)2=10√3m/s
t=sABuAB=√102+(10√3)210√3=2010√3
t=2√3 sec.
Topper's Solved these Questions
- BOOK - ALLENCHAPTER - KINEMATICSEXERCISE - EXERCISE-0155videos
KINEMATICS
- BOOK - ALLENCHAPTER - KINEMATICSEXERCISE - EXERCISE-0257videos
KINEMATICS
- BOOK - ALLENCHAPTER - ERROR AND MEASUREMENTEXERCISE - Part-2(Exercise-2)(B)22videos
ERROR AND MEASUREMENT
- BOOK - ALLENCHAPTER - KINEMATICS (MOTION ALONG A STRAIGHT LINE AND MOTION IN A PLANE)EXERCISE - BEGINNER S BOX-78videos
KINEMATICS (MOTION ALONG A STRAIGHT LINE AND MOTION IN A PLANE)
Similar Questions
A charged particle +q of mass m is placed at a distanced from another charged particle -2q of mass 2m in a uniform magnetic field B as shown in Fig. 1.28. If the particles are projected towards each other with same speed v,

a. find the maximum value of projected speed vm so that the two particles do not collide.
b. find the time after which collision occurs between the particles if projection speed equals 2vm.
c. Assuming the collision to be perfectly inelastic, find the radius of the particle in subsequent motion. (Neglect the electric force between the charges.)View Solution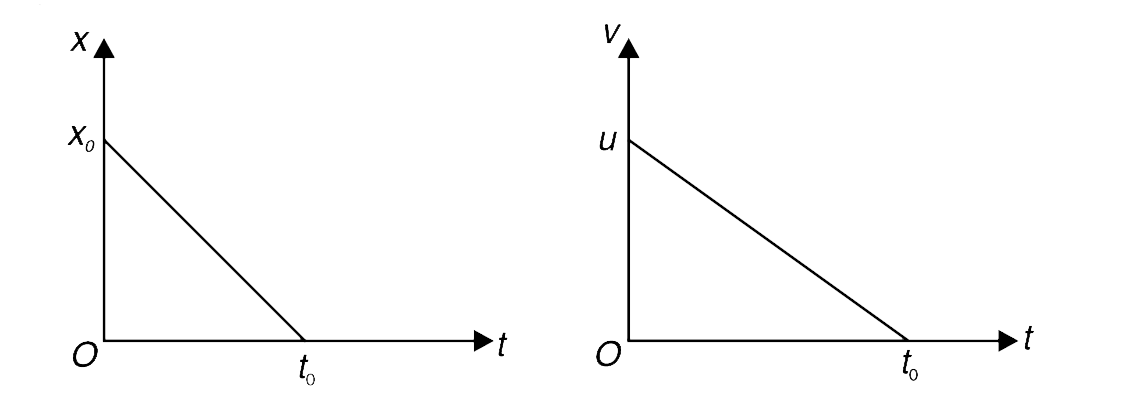
Two particles 1 and 2 move along the x axis. The position (x) - time (t) graph for particle 1 and velocity (v) - time (t) graph for particle 2 has been shown in the figure. Find the time when the two particles collide. Also find the position (x) where they collide. It is given that x0=ut0, and that the particle 2 was at origin at t=0.View Solution
Knowledge Check
- Question 1 - Select One
Two particles are projected simultaneously from the level ground as shown figure. They may collide after a time :
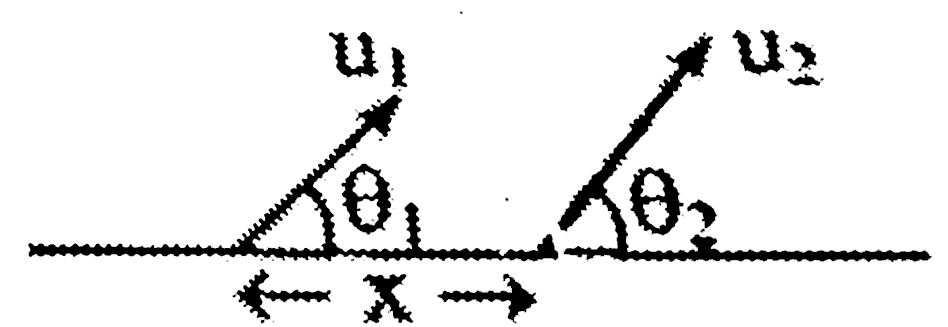 Axsinθ2u1Bxcosθ2u2Cxsinθ2u1sin(θ2−θ1)Dxsinθ1u2sin(θ2−θ1)
Axsinθ2u1Bxcosθ2u2Cxsinθ2u1sin(θ2−θ1)Dxsinθ1u2sin(θ2−θ1) - Question 2 - Select One
A particle is projected from the ground with speed u at angle 60∘ from horizontal. It collides with a second particle of same mass moving with horizontal speed u in same direction at highest point of its trajectory. If collision is perfectly inelastic then find horizontal distance travelled by them after collision when they reached at ground
A3√6u28gB3√3u28gCu28gD√3u2g
Two particles P and Q are projected from two points in the same plane as shown. Find the condition for collision of two paricles.
View SolutionA particle is projected with velocity "u" in horizontal direction as shown in the figure. Find u if particle collides perpendicularly with inclined plane. u
View SolutionA particle is projected with velocity "u" in horizontal direction as shown in the figure. Find u if particle collides perpendicularly with inclined plane. h
View SolutionA charged particle +q of mass m is placed at a distance d from another charge particle −2q of mass 2m in a uniform magnetic field of induction vectro B as shown in the fig.If the particles are projected towards each other with equal speeds v.(Neglect the interaction between the particles)
(a)Find the maximum value of the projection speed Vmax so that the two particles do not collide.
b)Find the time interval after which collision occurs between the particles if projection speed equals 2Vmax
(c)In the previous part,assuming that the particles stick after the collision find the radius of the circular path of the particle in subsequent motion.
 View Solution
View SolutionTwo particles A and B are projected simultaneously in a vertical plane as shown in figure. They collide at time t in air. Write down two necessary equations for collision to take place.
 View Solution
View SolutionA particle is projected along an inclined plane as shown in figure. What is the speed of the particle when it collides at point A ? (g=10m/s)
 View Solution
View Solution

