$ω_{A B} = \frac{Relative velocity of A w.r.t. B perpendicular to line AB}{Sepration between a and B}$
$∣ ∣ {({\to v}_{A B})}_{⊥} ∣ ∣ = v_{A} {sin θ}_{1} + v_{B} {sin θ}_{2}$
$r_{A B} = r$
$ω_{A B} = \frac{v_{A} {sin θ}_{1} + v_{B} {sin θ}_{2}}{r}$
${(v_{A B})}_{11} = v_{A} {cos θ}_{1} - v_{B} {cos θ}_{2}$
${(v_{A B})}_{11} > 0 .$ Then A will approach B
${(v_{A B})}_{11} < 0 .$ Then B will separate from A

Video Solution

Answer

Step by step video & image solution for omega_(AB)=("Relative velocity of A w.r.t. B perpendicular to line AB")/("Sepration between a and B") |(vec(v)_(AB))_(bot)|=v_(A) sin theta_(1)+v_(B) sin theta_(2) r_(AB)=r omega_(AB)=(v_(A) sin theta_(1)+v_(B) sin theta_(2))/(r) (v_(AB))_(11)=v_(A) cos theta_(1)-v_(B) cos theta_(2) (v_(AB))_(11) gt 0." " Then A will approach B (v_(AB))_(11) lt 0. " " Then B will separate from A by Physics experts to help you in doubts & scoring excellent marks in Class 11 exams.

Updated on:21/07/2023

Class 11 PHYSICS RECTILINEAR MOTION

Topper's Solved these Questions

Knowledge Check

Question 1 - Select One or More
Two particles of equal mass in are projected from the ground with speeds $v_{1}$ and $v_{2}$ at angles $θ_{1}$ , and $θ_{2}$ as shown in the figure. Given $θ_{2} > θ_{1}$ and $v_{1} {cos θ}_{1} = v_{2} {cos θ}_{2}$ Which statement/s is/are correct?

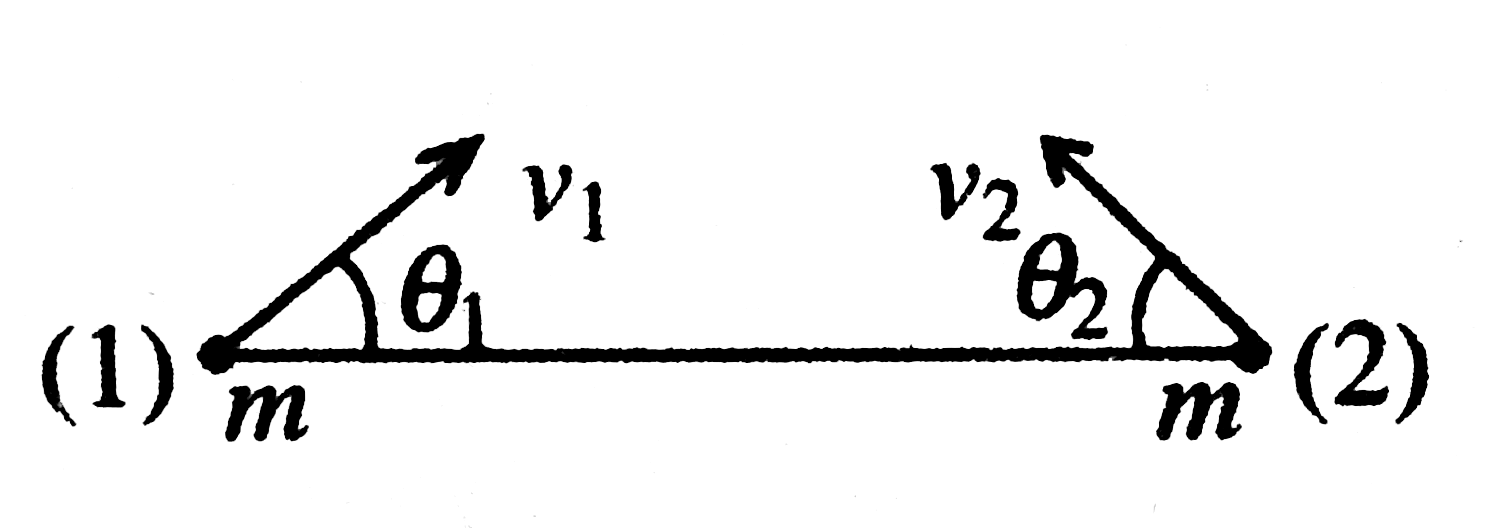ACentre of mass of particles will move along a vertical line.
BCentre of mass of particles will move along a line inclined at some angle with vertical.
CParticle $' 1'$ will be above vertical. centre of mass level when both particles are in air.
DParticle $' 2'$ will be above centre of mass level both particles are in air.
Question 2 - Select One
Two masses A and B are connected with two an inextesible string to write constraint relation between $v_{A} & v_{B}$

Student A : $v_{A} cos θ = v_{B}$
Student B : $v_{B} cos θ = v_{A}$
AA is correct, B is wrong
BB is correct, A is wrong
Cboth are correct
DBoth are wrong
Question 3 - Select One
If $u = (1 + cos θ) (1 + cos 2 θ) - sin θ . sin 2 θ, v = sin θ (1 + cos 2 θ) + sin 2 θ (1 + cos θ)$ , then $u^{2} + v^{2} =$
A $4 (1 + cos θ) (1 + cos 2 θ)$
B $4 (1 + sin θ) (1 + sin 2 θ)$
C $4 (1 - cos θ) (1 - cos 2 θ)$
D $4 (1 - sin θ) (1 - sin 2 θ)$

ALLEN-KINEMATICS-Integer Type Question

Home
Ask Doubt
Profile

ωAB=Relative velocity of A w.r.t. B perpendicular to line ABSepration between a and B ∣∣(→vAB)⊥∣∣=vAsinθ1+vBsinθ2 rAB=r ωAB=vAsinθ1+vBsinθ2r (vAB)11=vAcosθ1−vBcosθ2 (vAB)11>0. Then A will approach B (vAB)11<0. Then B will separate from A

Topper's Solved these Questions

Similar Questions

Knowledge Check

Two particles of equal mass in are projected from the ground with speeds v1 and v2 at angles θ1, and θ2 as shown in the figure. Given θ2>θ1 and v1cosθ1=v2cosθ2Which statement/s is/are correct?

Two masses A and B are connected with two an inextesible string to write constraint relation between vA&vB Student A : vAcosθ=vB Student B : vBcosθ=vA

If u=(1+cosθ)(1+cos2θ)−sinθ.sin2θ,v=sinθ(1+cos2θ)+sin2θ(1+cosθ), then u2+v2=

ALLEN-KINEMATICS-Integer Type Question

Two particles of equal mass in are projected from the ground with speeds $v_{1}$ and $v_{2}$ at angles $θ_{1}$ , and $θ_{2}$ as shown in the figure. Given $θ_{2} > θ_{1}$ and $v_{1} {cos θ}_{1} = v_{2} {cos θ}_{2}$ Which statement/s is/are correct?

Two masses A and B are connected with two an inextesible string to write constraint relation between $v_{A} & v_{B}$

Student A : $v_{A} cos θ = v_{B}$
Student B : $v_{B} cos θ = v_{A}$

If $u = (1 + cos θ) (1 + cos 2 θ) - sin θ . sin 2 θ, v = sin θ (1 + cos 2 θ) + sin 2 θ (1 + cos θ)$ , then $u^{2} + v^{2} =$