A particle is moving in a circular orbit when a constant tangential acceleration. After $2 s$ from the beginning of motion, angle between the total acceleration vector and the radius E becomes $45^{\circ}$ . What is the angular acceleration of the particle?

Video Solution

Text Solution

Verified by Experts

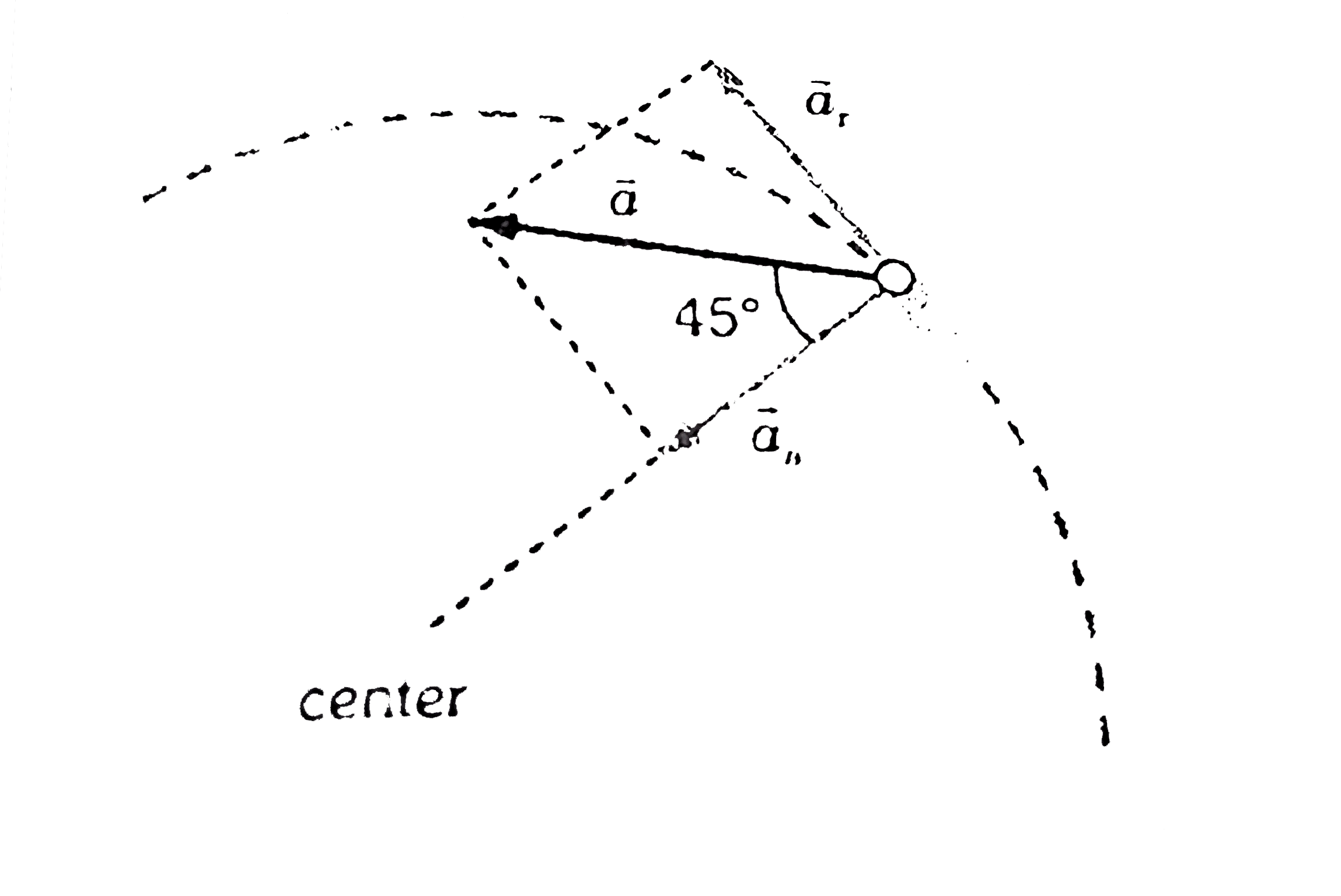
In the adjoining figure are shown the total acceleration vector $\to a$ and its components the tangential accelerations ${\to a}_{τ}$ and normal acceleration ${\to a}_{n}$ are shown. These two components are always mutually perpendicular to each other and act along the tangent to the circle and radius respectively. Therefore, if the total acceleration vector makes an angle of $45^{\circ}$ with the radius, both the tangential and the normal components must be equal in magnitudr.
Now from equation and, we have
$a_{τ} = a_{n} \to α R = ω^{2} R \Rightarrow α = ω^{2}$ ...(i)
Since angular acceleration is uniform, form equation, we have $ω = ω_{o} + α t$
Substituting $ω_{0} = 0$ and $t = 2 s$ , we have $ω = 2 α$ ...(ii)
From equation (i) and (ii), we have $α = 0.25 r a d / s^{2}$

Updated on:21/07/2023

A particle is moving in circular path with constant acceleration. In time t after the beginning of motion the direction of net acceleration is at $30^{\circ}$ to the radius vector at that instant. The angular acceleration of the particle at that time t is
A $\frac{3}{t^{2}}$
B $\frac{1}{t^{2}}$
C $\frac{\sqrt{3}}{t}$
D $\frac{\sqrt{3}}{t^{2}}$
A particle starts travelling on a circle with constant tangential acceleration. The angle between velocity vector and acceleration vector, at the moment when particle completes half the circular track. Is
A ${tan}^{- 1} (2 π)$
B ${tan}^{- 1} (π)$
C ${tan}^{- 1} (3 π)$
D ${tan}^{- 1} (2)$
A particle starts moving on circular path of radius $\frac{9}{4} m$ with tangential acceleration $3 m s^{- 2}$ . Find angle between acceleration of the particle and radius vector at time t=1 sec.
A $37^{\circ}$
B $53^{\circ}$
C $45^{\circ}$
D $60^{\circ}$