The total speed of a projectile at its greater height is √67 of its speed when it is at half of its greatest height. The angle of projection will be :-
60∘
45∘
30∘
50∘
The correct Answer is:C
v2y=u2sin2θ−2g×H2,v2x=u2cos2θ
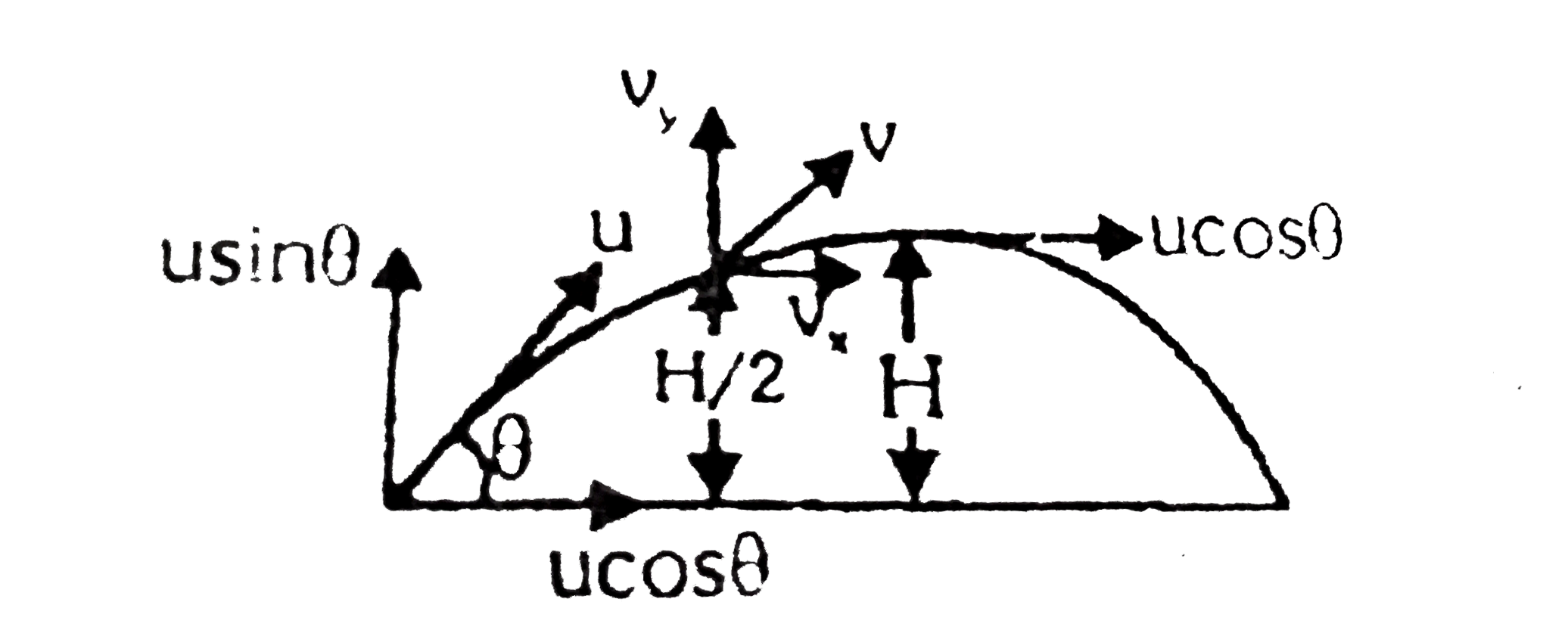
∴Ucosθ=√67[√v2x+v2y]⇒cosθ=√32 or θ=30∘
Topper's Solved these Questions
- BOOK - ALLENCHAPTER - KINEMATICSEXERCISE - EXERCISE-0257videos
KINEMATICS
- BOOK - ALLENCHAPTER - KINEMATICSEXERCISE - EXERCISE-036videos
KINEMATICS
- BOOK - ALLENCHAPTER - KINEMATICSEXERCISE - Integer Type Question3videos
KINEMATICS
- BOOK - ALLENCHAPTER - ERROR AND MEASUREMENTEXERCISE - Part-2(Exercise-2)(B)22videos
ERROR AND MEASUREMENT
- BOOK - ALLENCHAPTER - KINEMATICS (MOTION ALONG A STRAIGHT LINE AND MOTION IN A PLANE)EXERCISE - BEGINNER S BOX-78videos
KINEMATICS (MOTION ALONG A STRAIGHT LINE AND MOTION IN A PLANE)
Similar Questions
Knowledge Check
- Question 1 - Select One
The speed of a projectile when it is at its greatest height is √2/5 times its speed at half the maximum height. The angle of projection is
A30∘B60∘C45∘Dtan−1(3/4) - Question 2 - Select One
The velocity of a projectile when it is at the greatest height is (√2/5) times its velocity when it is at half of its greatest height. Determine its angle of projection.
Aθ=30∘Bθ=45∘Cθ=60∘Dθ=90∘ - Question 3 - Select One
The ratio of the speed of a projectile at the point of projection to the speed at the top of its trajectory is x. The angle of projection with the horizontal is
Asin1xBcos−1xCsin−1(1/x)Dcos−1(1/x)
The horizontal range of a projectile is times of its maximum height. Its angle of projection will be :-
View SolutionChoose the correct option
(i) The speed of a projectile at its maximum height is half of its initial speed. The angle of projection is 60∘.
(ii) A missile is fired for maximum range with an initial velocity of 20m/s, the range of the missile is 40m.
(iii) A ball is projected with a kinetic energy E at an angle of 45∘ to the horizontal. At the highest point during its flight, its kinetic energy will be E/2.
(iv) An object is projected at an angle of 45∘ with horizontal. The horizontal range and the maximum height will be in the ratio 4:1View SolutionThe speed of a projectile at its maximum height is √3/2 times its initial speed. If the range of the projectile is n times the maximum height attained by it, n is equal to :
View SolutionThe horizontal range of a projectile is 4√3 times its maximum height. Its angle of projection will be
View SolutionThe horizontal range of a projectile is 4√3 times its maximum height. The angle of projection is
View Solution

