In general if n is a natural a×a×a×a×...×a=ann - times a^n is called the nth power of a and is a also read as a raised to the n
To solve the problem of understanding the expression a×a×a×… (n times) and how it relates to exponents, we can break it down step by step.
1. Understanding the Expression:
- The expression a×a×a×… (where a is multiplied by itself n times) represents repeated multiplication of the number a.
Hint: Think of how many times you are multiplying the number a.
2. Defining the Exponent:
- This repeated multiplication can be expressed using exponents. Specifically, when you multiply a by itself n times, it can be written as an.
Hint: Remember that the exponent n indicates how many times the base a is used in multiplication.
3. Understanding the Notation:
- The notation an is read as "a raised to the power of n" or "the nth power of a". This means that a is the base and n is the exponent.
Hint: The base is the number being multiplied, and the exponent tells you how many times to multiply it.
4. Example for Clarity:
- For example, if n=5 and a=2, then 2×2×2×2×2 can be written as 25.
Hint: Try substituting different values for a and n to see how the expression changes.
5. Generalizing the Concept:
- In general, for any natural number n, the expression a×a×a×… (n times) is always equal to an.
Hint: This rule applies to any number, not just integers, as long as n is a natural number.
Summary:
The expression a×a×a×… (n times) is equivalent to an, where a is the base and n is the exponent indicating the number of times a is multiplied by itself.
- The expression a×a×a×… (where a is multiplied by itself n times) represents repeated multiplication of the number a.
- This repeated multiplication can be expressed using exponents. Specifically, when you multiply a by itself n times, it can be written as an.
- The notation an is read as "a raised to the power of n" or "the nth power of a". This means that a is the base and n is the exponent.
- For example, if n=5 and a=2, then 2×2×2×2×2 can be written as 25.
- In general, for any natural number n, the expression a×a×a×… (n times) is always equal to an.
The expression a×a×a×… (n times) is equivalent to an, where a is the base and n is the exponent indicating the number of times a is multiplied by itself.
Similar Questions
Knowledge Check
If 1×2×3×…….×n is denoted by
 , then
, then 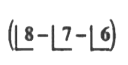 is equal to : A
is equal to : A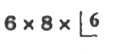 B
B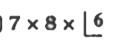 C
C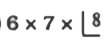 D
D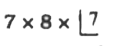
If (1×2×3×4×....×n!) = n, then (14! - 13! - 12!) is equal to
A14×12×(12!)B14×12×(13!)C14×13×(13!)D13×12×(12!)Let P(n):2n<(1×2×3×.....×n),n∈N. Then the smallest natural number n, for which P(n) is true is
A1B2C3D4
Find the whole number for which:
n×n=n
View SolutionIf A is a matrix of order m×n and B is a matrix such that ABT and BTA are both defined, then the order of matrix B is
View SolutionLet P(n):2n<(1×2×3×….×n) . Then the smallest positive integers for which P(n ) is true , is
View SolutionIf m times the mth term of an A.P. is equal to n times its nth term, find (m + n) th term of the A.P.:
View SolutionV = Constant × n' is -=
View Solution
