Interior opposite angles
Step by step video & image solution for Interior opposite angles by Maths experts to help you in doubts & scoring excellent marks in Class 7 exams.
Updated on:21/07/2023Similar Questions
The measure of one of the exterior angles of a triangle is twice one of the interior opposite angles and the measure of the other interior opposite angles is 60∘. The triangle is a/an
त्रिभुज के बाहरी कोणों में से एक का माप आंतरिक विपरीत कोणों से दोगुना है और कोण के विपरीत अन्य आंतरिक कोण का माप 60∘ है। त्रिभुज है?
View Solution(Exterior Angle Theorem): If a side of a triangle is produced, the exterior angle so formed is equal to the sum of the two interior opposite angles. GIVEN : A triangle ABC.D is a point of BC produced, forming exterior angle ∠4. TO PROVE : ∠4=∠1+∠2 i.e. , ∠ACD=∠CAB+∠CBA.
View Solution
Knowledge Check
If an exterior angle of a cyclic quadrilateral be 50∘, then the opposite interior angle is :
A130∘B40∘C50∘D90∘∠Aand∠B are the interior opposite angle of ∠BCD in ΔABC. Which of these statements is true?
 A∠BCA=∠BCD−∠AB∠A−180∘=∠BC∠A=90∘−∠BD∠B=∠BCD−∠A
A∠BCA=∠BCD−∠AB∠A−180∘=∠BC∠A=90∘−∠BD∠B=∠BCD−∠A
If the exterior angle of a quadrilateral formed by producing one of its sides is equal to the interior opposite angle, prove that the quadrilateral is cyclic.
View SolutionIf one side of a cyclic quadrilateral is produced, then the exterior angle is equal to the interior opposite angle.
View SolutionIf one side of a cyclic quadrilateral is produced; then the exterior angle is equal to the interior opposite angle.
View SolutionAn exterior angle of a triangle is 110∘, and one of the interior opposite angle is 30∘ . Then the other interior angle is K x 40∘. Find K.
View SolutionIn a triangle, an exterior angle at a vertex is 950 and its one of the interior opposite angle is 550 , then the measure of the other interior angle is 550 (b) 850 (c) 400 (d) 900
View SolutionIn the adjoining figure, identify(i) the pairs of corresponding angles.(ii) the pairs of alternate interior angles.(iii) the pairs of interior angles on the sameside of the transversal.(iv) the vertically opposite angles.
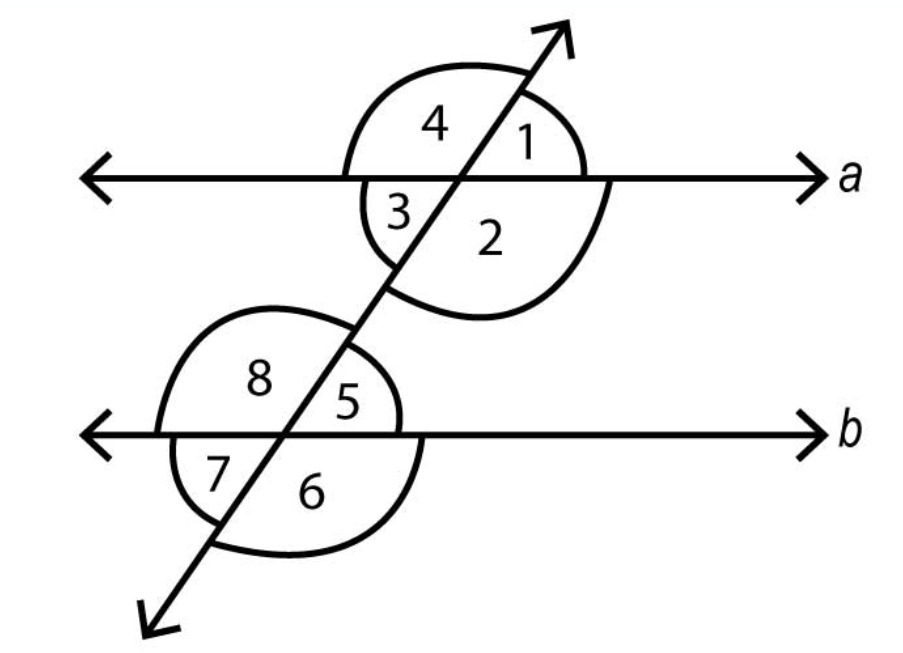
View Solution
