Theorem 2 prove that the sum of the interior angles of pentagon is 540∘.
To prove that the sum of the interior angles of a pentagon is 540∘, we can follow these steps:
Step 1: Understand the Structure of a Pentagon
A pentagon is a polygon with five sides. We denote the interior angles of the pentagon as A, B, C, D, and E.
Step 2: Draw a Diagonal
To find the sum of the interior angles, we can draw a diagonal. For example, we can draw a diagonal from vertex C to vertex E. This diagonal divides the pentagon into two parts: a triangle DEC and a quadrilateral ABCE.
Step 3: Calculate the Sum of Angles in the Quadrilateral
The sum of the interior angles of a quadrilateral is known to be 360∘. Therefore, for the quadrilateral ABCE:
A+B+∠AEC+∠BCE=360∘
Step 4: Calculate the Sum of Angles in the Triangle
The sum of the interior angles of a triangle is 180∘. For triangle DEC:
D+∠DEC+∠DCE=180∘
Step 5: Add the Two Equations
Now, we can add the two equations obtained from the quadrilateral and the triangle:
1. From the quadrilateral: A+B+∠AEC+∠BCE=360∘ (Equation 1)
2. From the triangle: D+∠DEC+∠DCE=180∘ (Equation 2)
Adding these two equations gives:
(A+B+∠AEC+∠BCE)+(D+∠DEC+∠DCE)=360∘+180∘
Step 6: Simplify the Left Side
On the left side, we can combine the angles:
A+B+C+D+E=540∘
where C is formed by adding ∠AEC and ∠BCE and E is formed by adding ∠DEC and ∠DCE.
Step 7: Conclusion
Thus, we have proven that the sum of the interior angles of a pentagon is:
A+B+C+D+E=540∘
A pentagon is a polygon with five sides. We denote the interior angles of the pentagon as A, B, C, D, and E.
To find the sum of the interior angles, we can draw a diagonal. For example, we can draw a diagonal from vertex C to vertex E. This diagonal divides the pentagon into two parts: a triangle DEC and a quadrilateral ABCE.
The sum of the interior angles of a quadrilateral is known to be 360∘. Therefore, for the quadrilateral ABCE:
A+B+∠AEC+∠BCE=360∘
The sum of the interior angles of a triangle is 180∘. For triangle DEC:
D+∠DEC+∠DCE=180∘
Now, we can add the two equations obtained from the quadrilateral and the triangle:
1. From the quadrilateral: A+B+∠AEC+∠BCE=360∘ (Equation 1)
2. From the triangle: D+∠DEC+∠DCE=180∘ (Equation 2)
(A+B+∠AEC+∠BCE)+(D+∠DEC+∠DCE)=360∘+180∘
On the left side, we can combine the angles:
A+B+C+D+E=540∘
where C is formed by adding ∠AEC and ∠BCE and E is formed by adding ∠DEC and ∠DCE.
Thus, we have proven that the sum of the interior angles of a pentagon is:
A+B+C+D+E=540∘
Similar Questions
Knowledge Check
The sum of all interior angles of a hexagon is
A6 right ∠sB8 right ∠sC9 right ∠sD12 right ∠sFind the sum of all the interior angles of a pentagon
A450∘B180∘C360∘D540∘The sum of the measure of the interior angles of a polygon is 540∘. Find the number of sides of the polygon.
A8B7C6D5
Prove that the sum of the interior angles of an octagon is twice the sum of interior angles of a pentagon
View SolutionFind the sum of the interior angles of the polygon gives below.
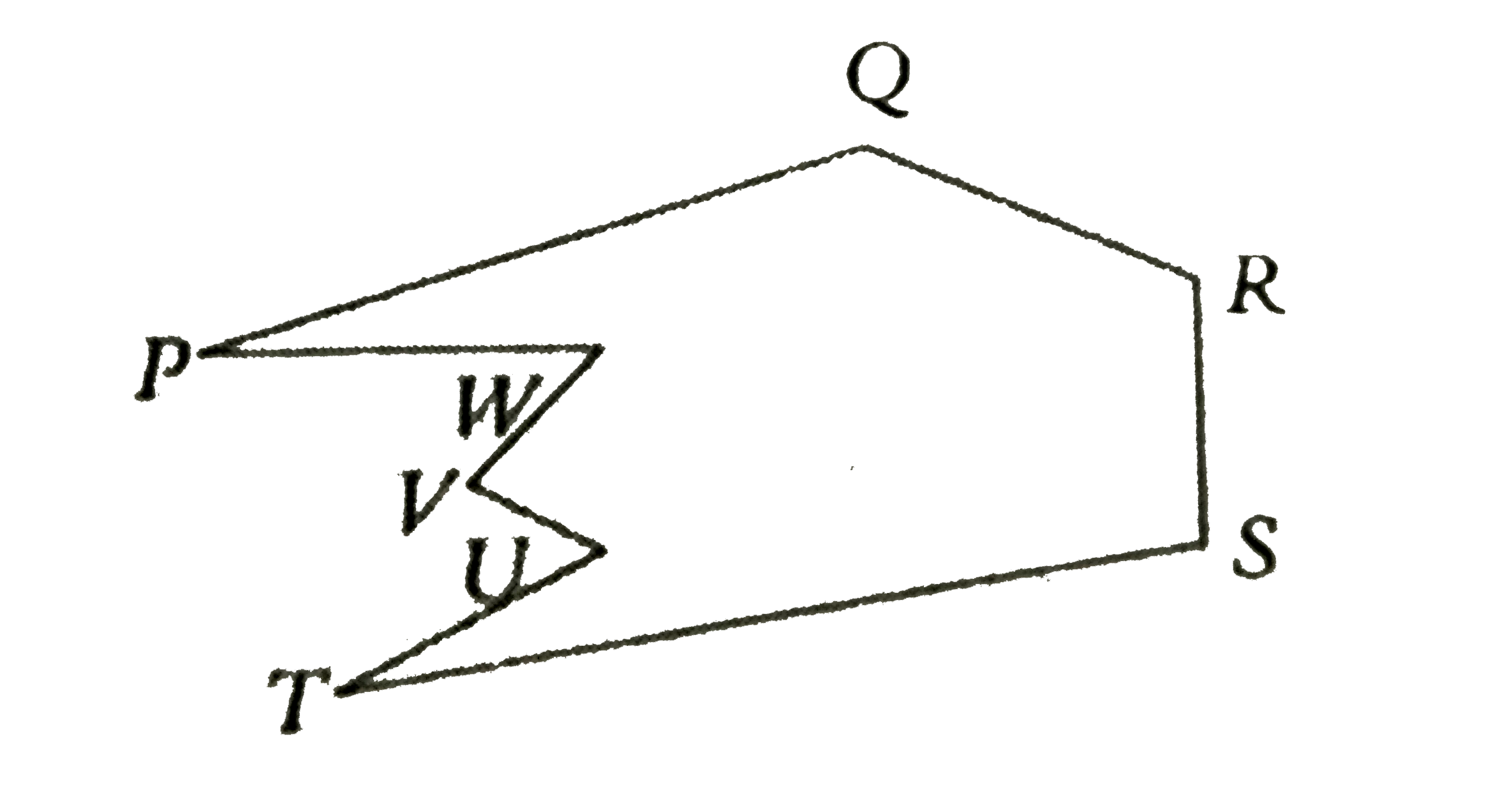
View SolutionFind the sum of the interior angles of a polygon of 8 sides.
View SolutionThe sum of the measure of the interior angles of a polygon is 540∘. Find the number of sides of the polygon.
View SolutionWhat is the sum of all the interior angles of the figure ?

View Solution
