Square
Step by step video & image solution for Square by Maths experts to help you in doubts & scoring excellent marks in Class 8 exams.
Updated on:21/07/2023Similar Questions
In figure XY∣∣ seg AC. If 2AX=3BX and XY=9, complete the activity to find the value of AC.
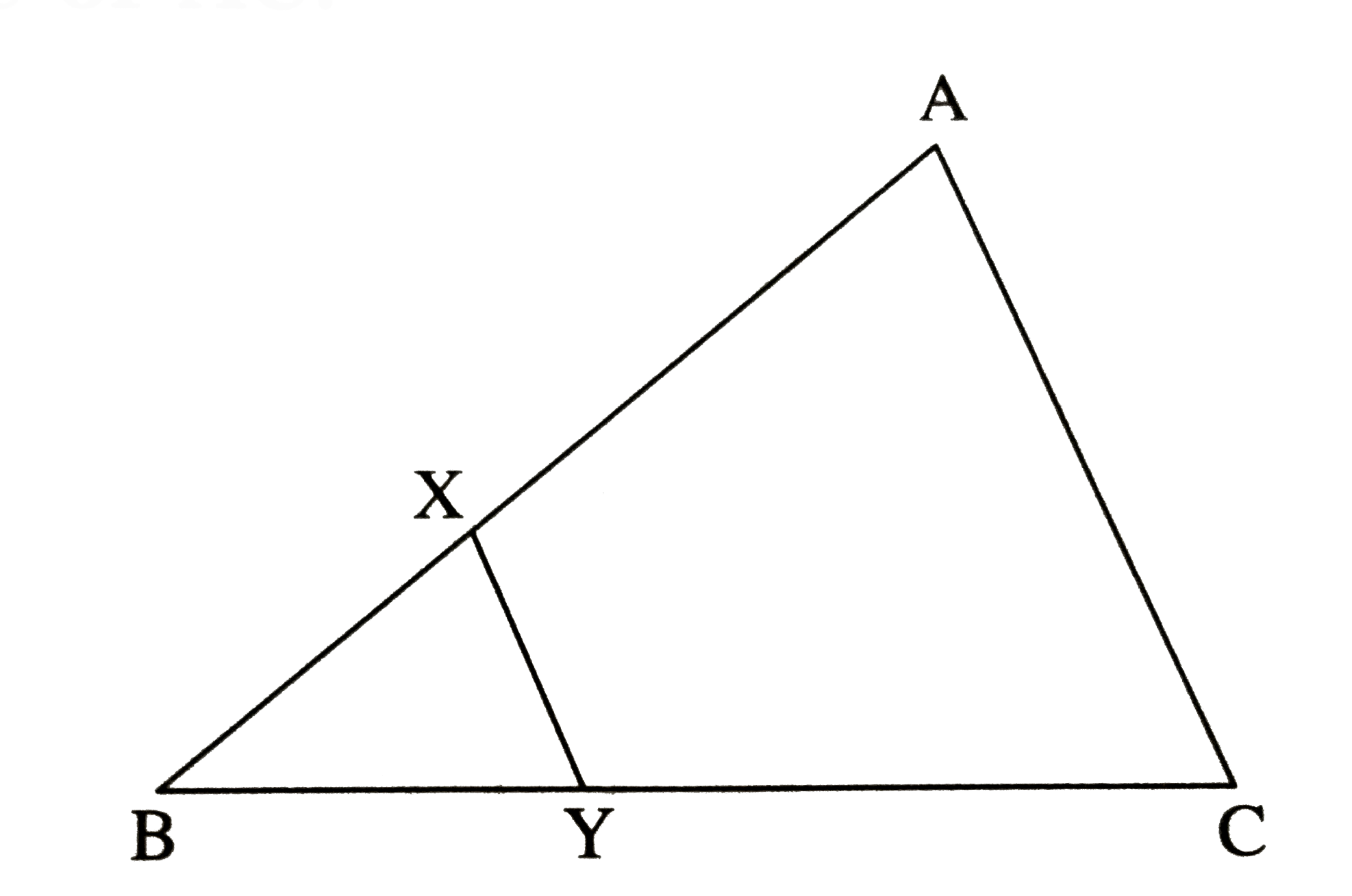
Activity: 2AX=3BX
∴AXBX=□□
∴AX+BXBX=□+□□.........(By componendo)
∴ABBX=□□.............1
ΔBCA~ΔBYX.......(□ test of similarity)
∴BABX=ACXY
..............(Corresponding sides of similar triangles)
∴□□=AC9
∴AC=□ ...........[From 1]
View SolutionA circle, a square and an equilateral triangle have the same area. The correct increasing order of the perimeters will be (a) triangle, square, circle (b) triangle, circle, square (c) circle, triangle, square (d) circle, square, triangle
View Solution
Knowledge Check
A square is drawn by joining mid pint of the sides of a square. Another square is drawn inside the second square in the same way and the process is continued in definitely. If the side of the first square is 16 cm, then what is the sum of the areas of all the squares ?
A256 sq cmB512 sq cmC1024 sq cmD512/3 sq cmA square is drawn by joining mid-points of the sides of a square. Another square is drawn inside the second square in the same way and the process is continued indefinitely. If the side of the first square is 16 cm, then what is the sum of the areas of all the squares ?
(a)256sq. Cm
(b)512 sq. cm
(c)1024sq. Cm
(d)512/3sq. CmA256sq. CmB512 sq. cmC1024sq. CmD512/3sq. CmThe length of side of a square is 'a' metre. A second square is formed by joining the middle points of this square. Then a third square is formed by joining the middle points of the sides of the second square and so on. Then, the sum of the areas of squares which carried upto infinity, is
Aa2B2a2C3a2D4a2
A side of a square is 16 cm. A new square is formed by joining the midpoints of sides, again a new square is formed by joining the mid-points of the new square and this process goes on till infiity. Find the total area of such square formed ?
View SolutionIn the figure shown square II is formed by joining the mid-points of square II
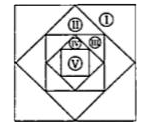
and so on . In this way total five squares are drawn . The sides of the square I is 'a' cm.
What is the total area of all the five squares ?
View Solution
