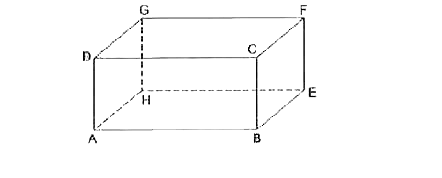
Name the pairs of all possible parallel edges of the pencil box whose figure is shown in Figure.
To solve the problem of naming the pairs of all possible parallel edges of a pencil box, we will analyze the edges of the box step by step.
1. Identify the Edges of the Box:
A pencil box is typically a rectangular prism (cuboid) with 12 edges. Let's label the edges as follows:
- Front face: AB, BC, CD, DA
- Back face: EF, FG, GH, HE
- Vertical edges: AD, BE, CF, DG
2. Group the Parallel Edges:
- Group 1: Identify edges that are parallel to each other on the same plane.
- AB is parallel to EF
- CD is parallel to GH
- DA is parallel to FG
- BC is parallel to HE
- Thus, we can say:
- AB || EF
- CD || GH
- DA || FG
- BC || HE
3. Group 2: Identify the vertical edges that are parallel to each other.
- AD is parallel to BE
- BC is parallel to CF
- CD is parallel to DG
- DA is parallel to EH
- Thus, we can say:
- AD || BE
- BC || CF
- CD || DG
- DA || EH
4. Group 3: Identify the edges that are parallel to each other on the opposite faces.
- DG is parallel to CF
- AH is parallel to BE
- DA is parallel to GH
- EF is parallel to CB
- Thus, we can say:
- DG || CF
- AH || BE
- DA || GH
- EF || CB
5. Final Listing of Parallel Edges:
- Group 1: AB || EF, CD || GH, DA || FG, BC || HE
- Group 2: AD || BE, BC || CF, CD || DG, DA || EH
- Group 3: DG || CF, AH || BE, DA || GH, EF || CB
Conclusion:
The pairs of all possible parallel edges of the pencil box can be grouped into three groups as follows:
- Group 1: AB || EF, CD || GH, DA || FG, BC || HE
- Group 2: AD || BE, BC || CF, CD || DG, DA || EH
- Group 3: DG || CF, AH || BE, DA || GH, EF || CB
A pencil box is typically a rectangular prism (cuboid) with 12 edges. Let's label the edges as follows:
- Front face: AB, BC, CD, DA
- Back face: EF, FG, GH, HE
- Vertical edges: AD, BE, CF, DG
- Group 1: Identify edges that are parallel to each other on the same plane.
- AB is parallel to EF
- CD is parallel to GH
- DA is parallel to FG
- BC is parallel to HE
- Thus, we can say:
- AB || EF
- CD || GH
- DA || FG
- BC || HE
- AD is parallel to BE
- BC is parallel to CF
- CD is parallel to DG
- DA is parallel to EH
- Thus, we can say:
- AD || BE
- BC || CF
- CD || DG
- DA || EH
- DG is parallel to CF
- AH is parallel to BE
- DA is parallel to GH
- EF is parallel to CB
- Thus, we can say:
- DG || CF
- AH || BE
- DA || GH
- EF || CB
- Group 1: AB || EF, CD || GH, DA || FG, BC || HE
- Group 2: AD || BE, BC || CF, CD || DG, DA || EH
- Group 3: DG || CF, AH || BE, DA || GH, EF || CB
The pairs of all possible parallel edges of the pencil box can be grouped into three groups as follows:
- Group 1: AB || EF, CD || GH, DA || FG, BC || HE
- Group 2: AD || BE, BC || CF, CD || DG, DA || EH
- Group 3: DG || CF, AH || BE, DA || GH, EF || CB
Topper's Solved these Questions
Similar Questions
Knowledge Check
Identify the figure shown in figure:
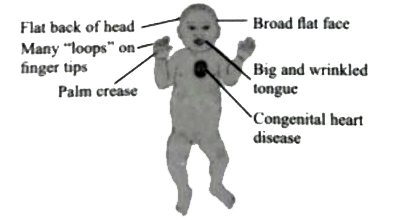 AKlinefelter's syndromeBDown's syndromeCTurner's syndromeDPhenylketonuria
AKlinefelter's syndromeBDown's syndromeCTurner's syndromeDPhenylketonuria
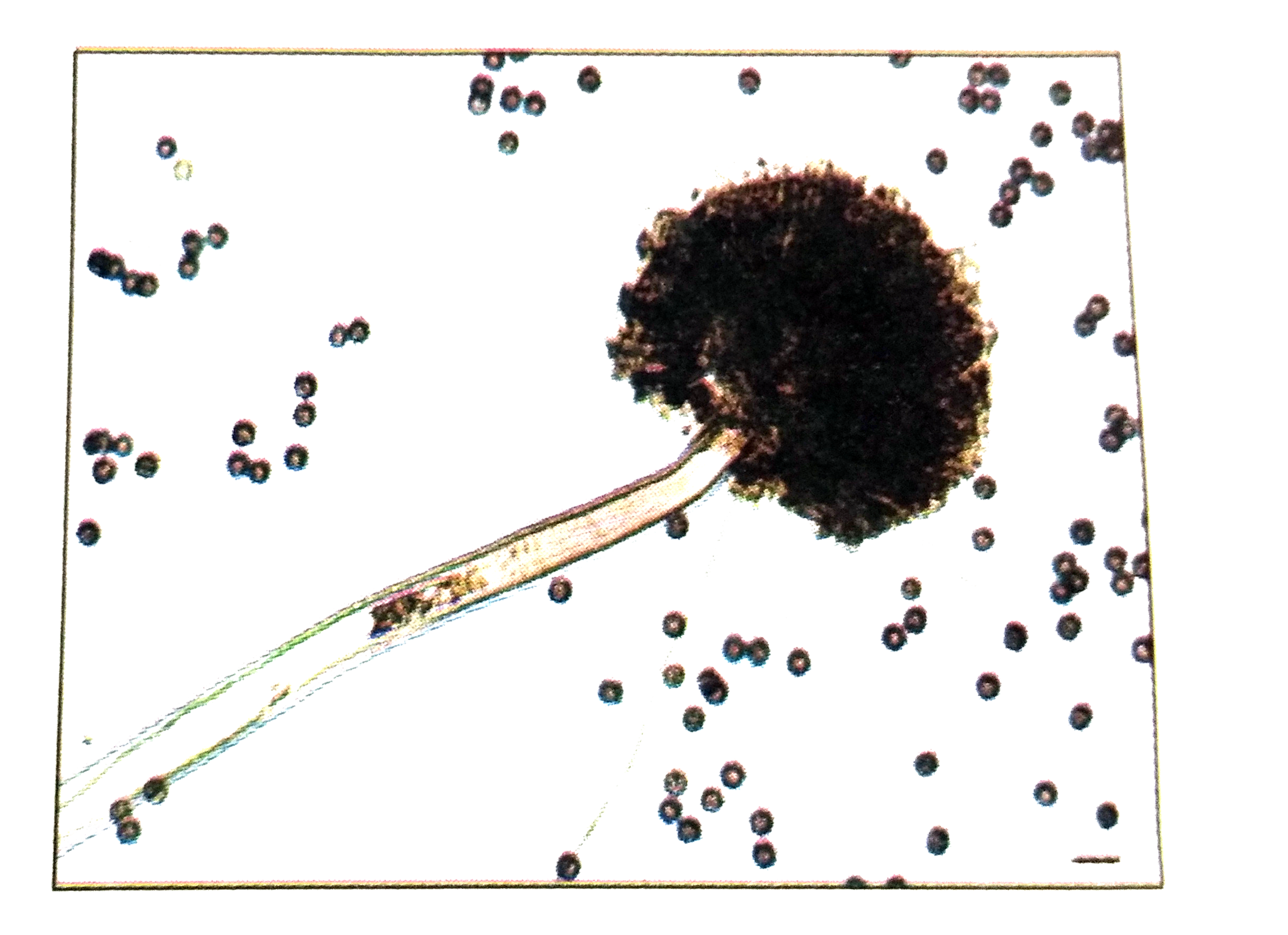
What is the name of the microbe shown in the figure?
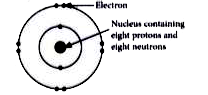
View SolutionName the particle whose electronic arrangement is shown in figure.
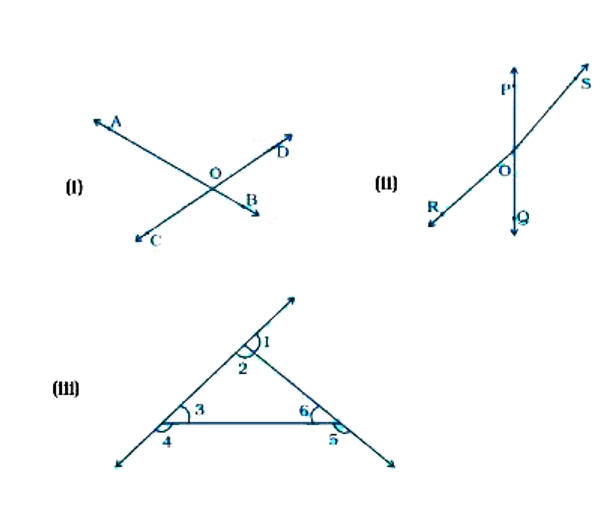
View SolutionName all the angles formed in Figure
View SolutionName the pairs of supplementary angles in the following figures:
View SolutionName the mechanism of seed dispersal shown in the given figure
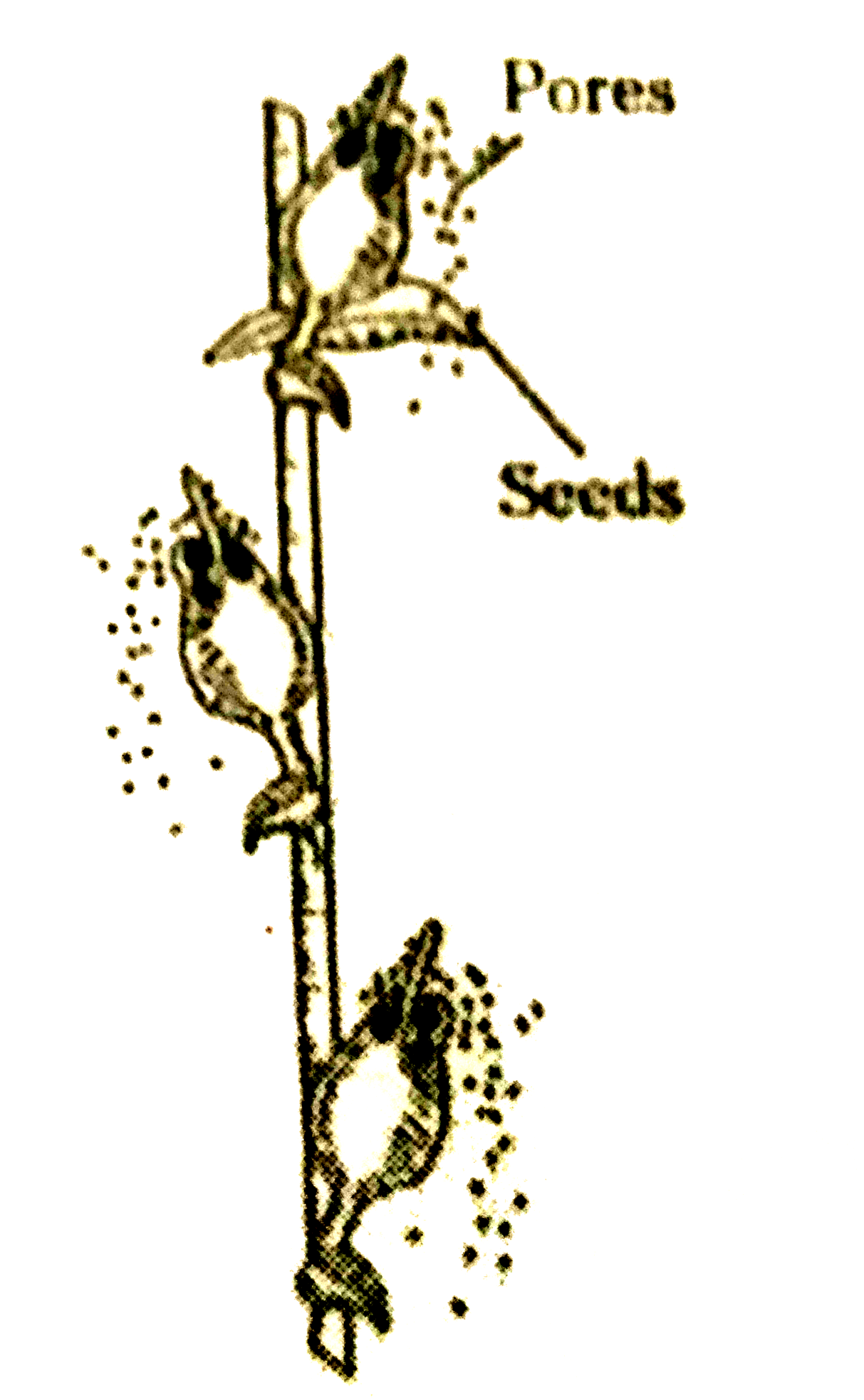
View SolutionThe number of edges in the given figure is

View SolutionFrom Figure, name All pairs of parallel lines. all pairs of intersecting lines. lines of whose point of intersection in P lines whose point of intersection in C lines whose point of intersection in R Collinear points.
View Solution