In Fig.23, OA and OB are opposite rays: (i) If (ii)(iii)x=(iv)(v)25(vi)0(vii)(viii),(ix) (x) what is the value of (xi)(ξi)y?(ξii) (xiv) (xv) If (xvi)(xvii)y=(xviii)(ξx)35(xx)0(xxi)(xxii),(×iii) (xxiv) what is the value of (xxv)(×vi)x?(×vii) (xxviii)
Step by step video & image solution for In Fig.23, O A\ a n d\ O B are opposite rays: (i) If ( i i ) (iii) x=( i v ) (v) 25^(( v i )0( v i i ))( v i i i ) , (ix) (x) what is the value of ( x i ) (xii) y ? (xiii) (xiv) (xv) If ( x v i ) (xvii) y=( x v i i i ) (xix) 35^(( x x )0( x x i ))( x x i i ) , (xxiii) (xxiv) what is the value of ( x x v ) (xxvi) x ? (xxvii) (xxviii) by Maths experts to help you in doubts & scoring excellent marks in Class 7 exams.
Updated on:21/07/2023Topper's Solved these Questions
Similar Questions
In Fig.78, we have (i) (ii)(iii)∠MLY=2∠LMQ,(iv) (v) find (vi)(vii)∠LMQ(viii) (ix) (x) (xi)(ξi)∠XLM=(xiii)(ξv)((xv)(xvi)2x−10(xvii))(xviii)0(xix)(xx)(×i) (xxii) and (xxiii)(×iv)∠LMQ=x+(xxv)(×vi)30(xxvii)0(xxviii)(xxix),(×x) (xxxi) find (xxxii)(×ξii)x.xxxiv (xxxv) (xxxvi) (xxxvii)(×xviii)∠XLM=∠PML, (xxxix) (xl) find (xli)(xlii)∠ALY(xliii) (xliv) (xlv) (xlvi)(xlvii)∠ALY=(xlviii)(xlix)((l)(li)2x−15(lii))(liii)0(liv)(lv), ∠LMQ=(lvi)(lvii)((lviii)(lix)x+40(lx))(lxi)0(lxii)(lxiii),(lξv) (lxv) find (lxvi)(lxvii)x.lxviii (lxix)
View Solutioni.
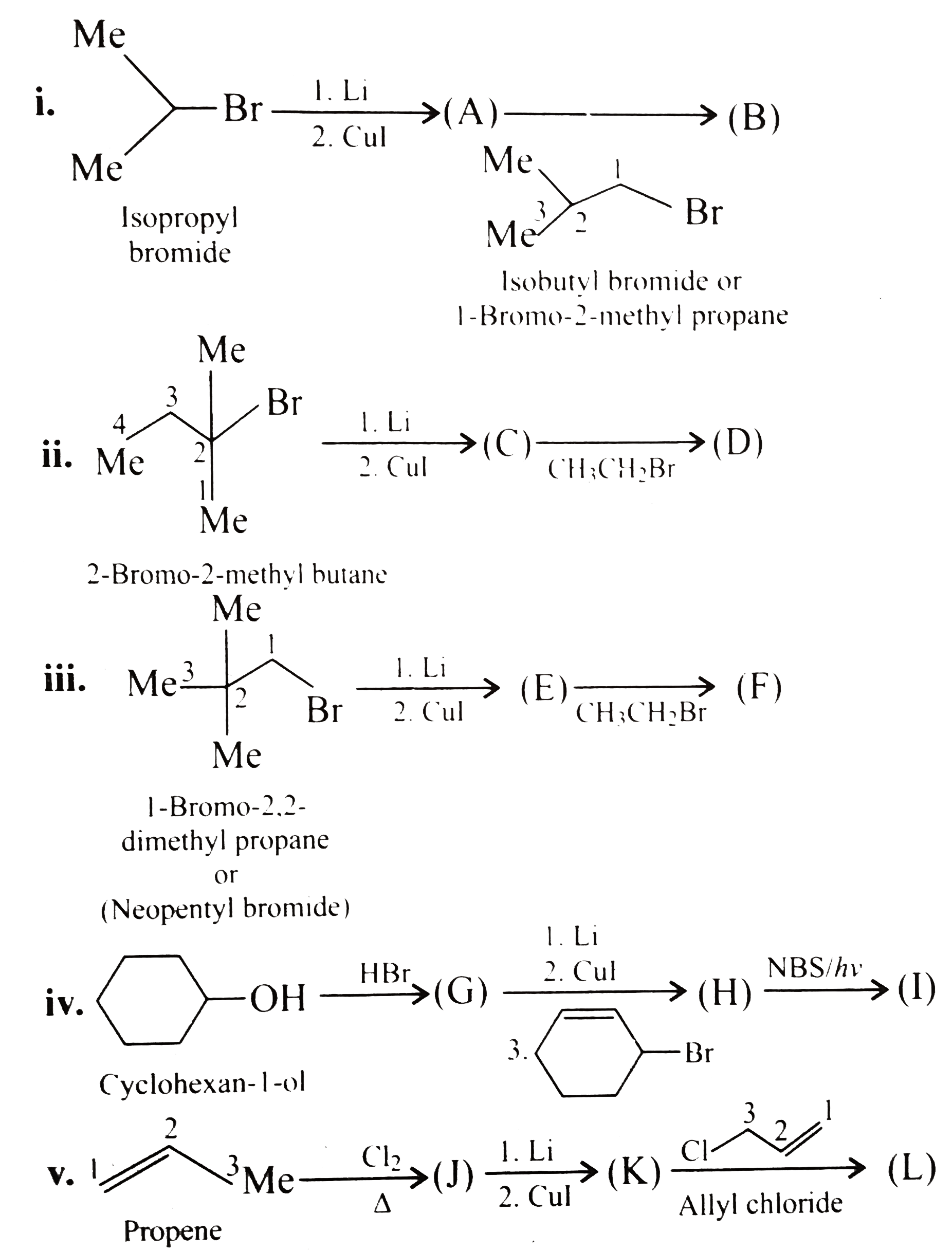
ii.
iii.
iv.
iv.
v.
View Solution
Knowledge Check
If (1+i)x−2i3+i+(2−3i)y+i3−i=i then the real value of x and y are given by
Ax = - 3, y = - 1Bx= 3, y = - 1Cx = 3, y = 1Dx= 1, y = - 3
(v)(1−i)2(1+i)−(3−4i)2
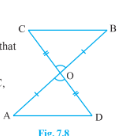
View SolutionIn Fig. 7.8, OA = OBand OD = OC. Show that (i)ΔAOD≅ΔBOC and (ii)AD ∣∣ BC.
View SolutionFind the square root of the following :
(i) 3−4i
(ii) 4+6i√5
(iii) −i
(iv) 8i
(v) −7+24i
(vi) −24−10i
View SolutionFind the values of xandy: (i) x+3i=6−9iy (ii) (x+iy)−(3−2i)=5+i (iii) i=x+2yi (iv) 4x+i(x−y)=2−5i (v) (x+2iy)(2−i)2=10(1−i)
View SolutionSimplify the following :
(i) i97
(ii) i8
(iii) 1i3
(iv) (−i)14
(v) i−22
(vi) i−63
View SolutionIdentify:
i.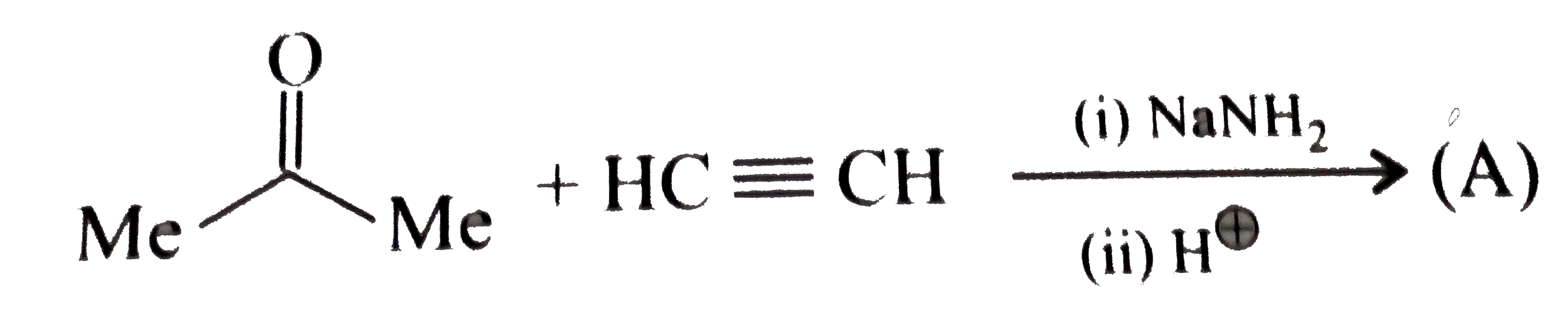
ii.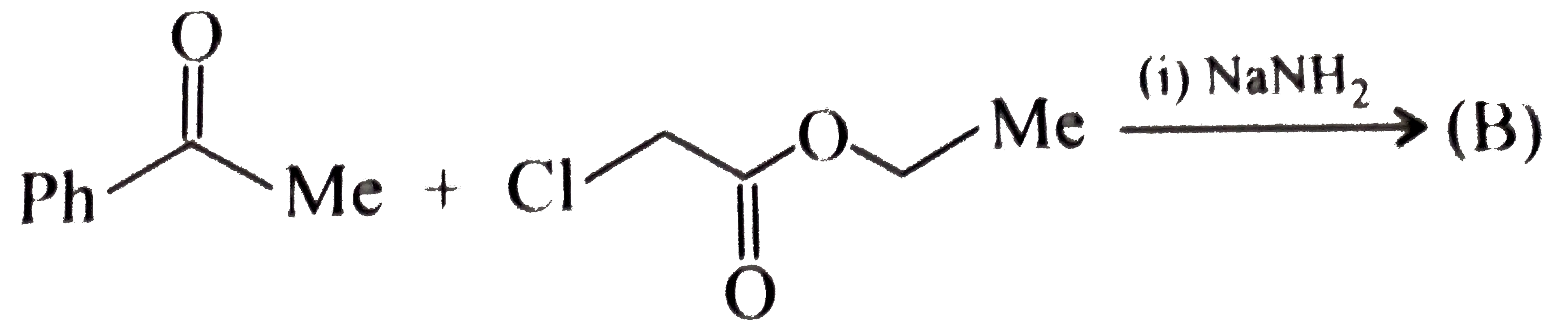
iii.
iv.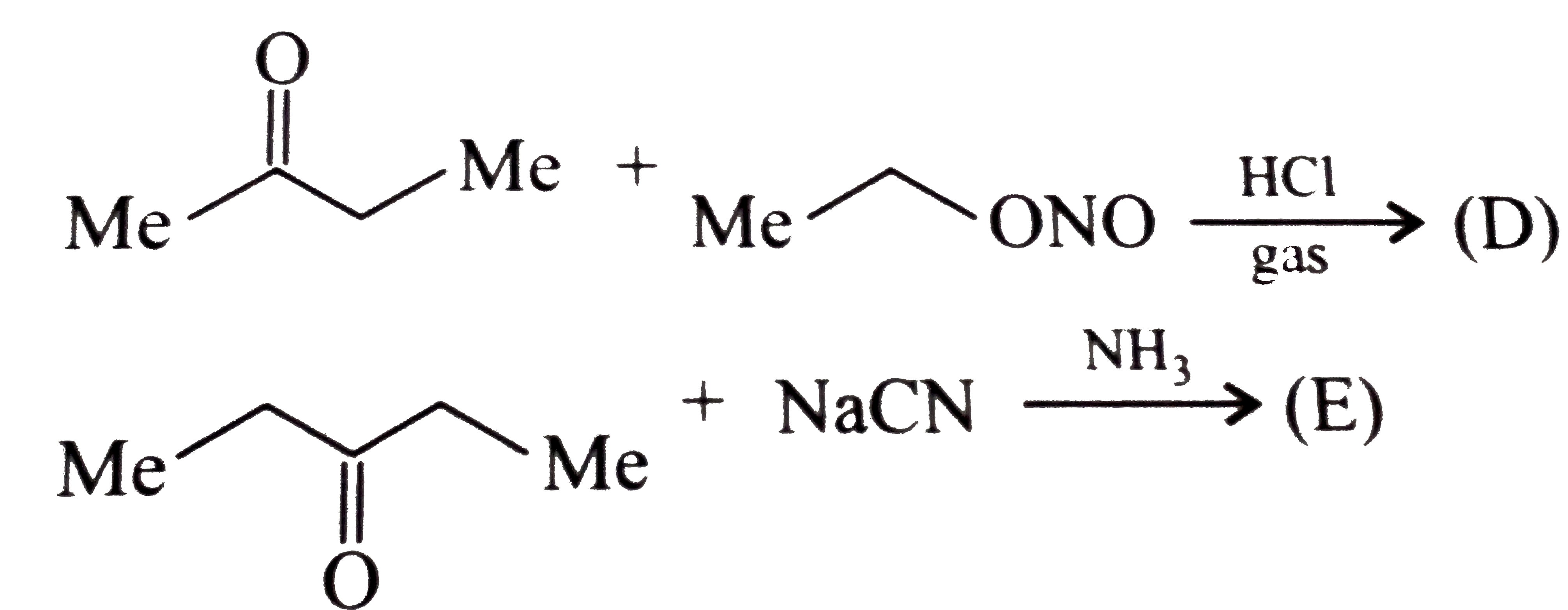
v.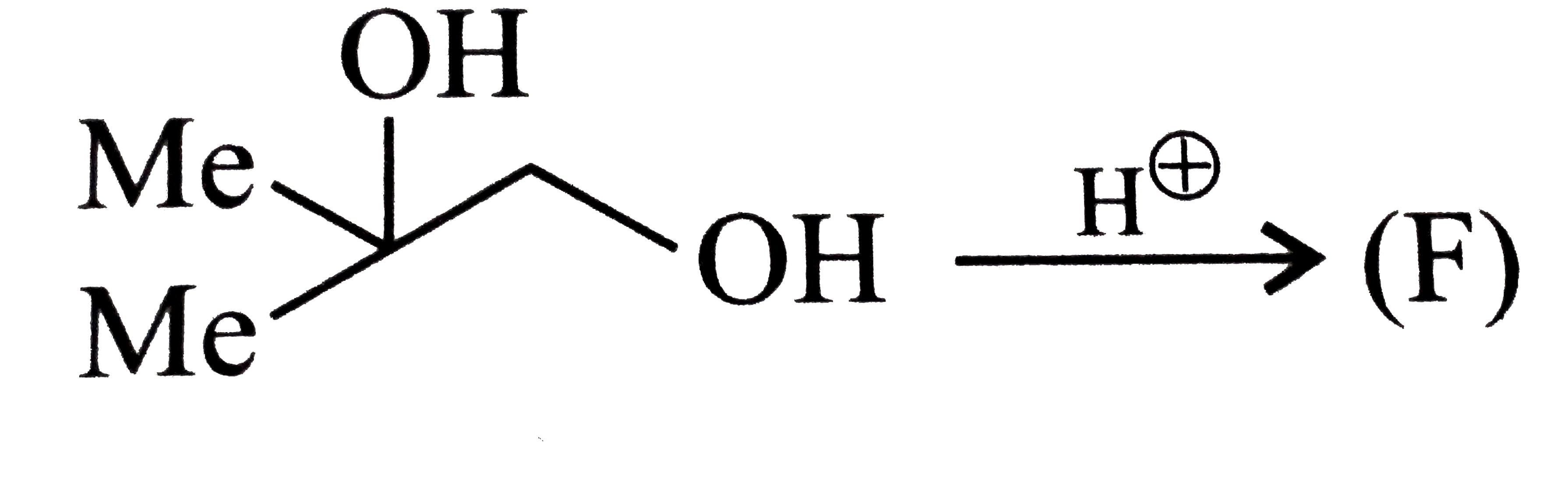
vi.
View SolutionEvaluate the following :
(i) i7
(ii) i51
(iii) 1i
(iv) i−71
(v) (i37+1i67)
View Solution
