In Fig.76, ABCD. Find the value of x,y,z.
To solve the problem, we need to find the values of angles x, y, and z given that lines AB and CD are parallel and AC and BD are transversal lines.
1. Identify the Angles:
- We have angle x and angle 125∘ on the same straight line. Since they are linear pairs, their sum is 180∘.
x+125∘=180∘
2. Solve for x:
- Rearranging the equation gives:
x=180∘−125∘=55∘
3. Identify the Relationship between x and z:
- Angles x and z are on the same side of the transversal AC and are interior angles. Therefore, their sum is also 180∘.
x+z=180∘
4. Substitute the Value of x:
- We already found x=55∘:
55∘+z=180∘
5. Solve for z:
- Rearranging gives:
z=180∘−55∘=125∘
6. Identify the Relationship between x and y:
- Angles y and 125∘ are also on the same side of the transversal BD. Thus, their sum is 180∘.
y+125∘=180∘
7. Solve for y:
- Rearranging gives:
y=180∘−125∘=55∘
Final Values:
- x=55∘
- y=55∘
- z=125∘
- We have angle x and angle 125∘ on the same straight line. Since they are linear pairs, their sum is 180∘.
- Rearranging the equation gives:
- Angles x and z are on the same side of the transversal AC and are interior angles. Therefore, their sum is also 180∘.
- We already found x=55∘:
- Rearranging gives:
- Angles y and 125∘ are also on the same side of the transversal BD. Thus, their sum is 180∘.
- Rearranging gives:
- x=55∘
- y=55∘
- z=125∘
Topper's Solved these Questions
Similar Questions
In Fig.65, lm and pq. Find the value of x,y,z,t.
View SolutionIn Fig.85, ABCD and ACBD. Find the value of x,y,z.
View SolutionIn fig. 67, l∈e lm. Find the value of a,b,c,.. Give reasons.
View SolutionFind the value of x in Fig. 6.38
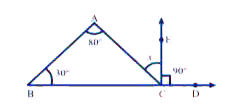
View SolutionIn Fig.71, if ABCD, then the values of x, y and z are x=56, y=47, z=77 (b) x=47, y=56, z=77 x=77, y=56, z=47 (d) x=56, y=77, z=47
View SolutionIn Fig.84, ABCD and AECF; ∠FCG=900 and ∠BAC=1200. Find the values of x,y and z.
View SolutionFind the values of x and y in Fig. 6.37
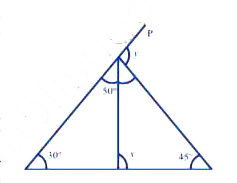
View SolutionIn Fig.ABCD is a rectangle. Find the values of x and y

View SolutionIn Fig, ABCD is a rectangle. Find the values of x and y.

View SolutionIn the given fig. AB∣∣CD. Find the value of x.
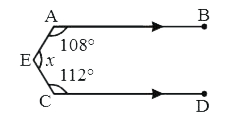
View Solution
