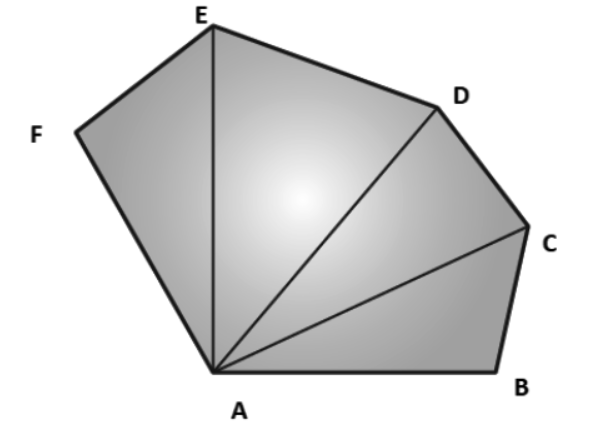
In five cornered fig. 18,AD,AC are joined. Find ∠EAB+∠BAC+∠BCD+∠CDE+∠DEA .
To solve the problem of finding the sum of the angles ∠EAB+∠BAC+∠BCD+∠CDE+∠AED in the five-cornered figure, we can follow these steps:
1. Identify the Triangles:
In the five-cornered figure, we can identify three triangles: △ABC, △ADC, and △AED.
2. Apply the Angle Sum Property:
According to the angle sum property of triangles, the sum of the angles in a triangle is always 180∘.
3. Write the Equations for Each Triangle:
- For triangle ABC:
∠ABC+∠BAC+∠ACB=180∘(Equation 1)
- For triangle ADC:
∠ADC+∠DAC+∠ACD=180∘(Equation 2)
- For triangle AED:
∠AED+∠ADE+∠DAE=180∘(Equation 3)
4. Add the Equations:
Now, we add all three equations:
(∠ABC+∠BAC+∠ACB)+(∠ADC+∠DAC+∠ACD)+(∠AED+∠ADE+∠DAE)=180∘+180∘+180∘
This simplifies to:
∠ABC+∠BAC+∠ACB+∠ADC+∠DAC+∠ACD+∠AED+∠ADE+∠DAE=540∘
5. Rearranging the Angles:
We can rearrange the angles in the equation:
- Notice that ∠BAC+∠DAC+∠DAE can be combined as ∠EAB.
- The angles ∠ACB and ∠ACD remain as they are.
- The angles ∠ABC and ∠AED remain as they are.
6. Final Expression:
Thus, we can express the sum as:
∠ABC+∠EAB+∠BCD+∠CDE+∠AED=540∘
Conclusion:
The sum of the angles ∠EAB+∠BAC+∠BCD+∠CDE+∠AED is equal to 540∘.
In the five-cornered figure, we can identify three triangles: △ABC, △ADC, and △AED.
According to the angle sum property of triangles, the sum of the angles in a triangle is always 180∘.
- For triangle ABC:
∠ABC+∠BAC+∠ACB=180∘(Equation 1)
- For triangle ADC:
∠ADC+∠DAC+∠ACD=180∘(Equation 2)
- For triangle AED:
∠AED+∠ADE+∠DAE=180∘(Equation 3)
Now, we add all three equations:
(∠ABC+∠BAC+∠ACB)+(∠ADC+∠DAC+∠ACD)+(∠AED+∠ADE+∠DAE)=180∘+180∘+180∘
This simplifies to:
∠ABC+∠BAC+∠ACB+∠ADC+∠DAC+∠ACD+∠AED+∠ADE+∠DAE=540∘
We can rearrange the angles in the equation:
- Notice that ∠BAC+∠DAC+∠DAE can be combined as ∠EAB.
- The angles ∠ACB and ∠ACD remain as they are.
- The angles ∠ABC and ∠AED remain as they are.
Thus, we can express the sum as:
∠ABC+∠EAB+∠BCD+∠CDE+∠AED=540∘
The sum of the angles ∠EAB+∠BAC+∠BCD+∠CDE+∠AED is equal to 540∘.
Topper's Solved these Questions
Similar Questions
Knowledge Check
A,B,C,D and E are five
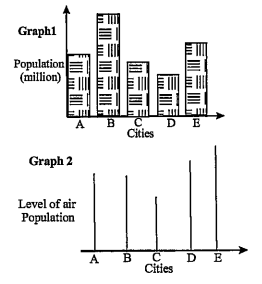 AThe bigger the population of people living in a city the higher the level of air pollution in that cityBThe land is more polluted in city A than in city CCCity E contains the most pollutants in the airDThe air pollution in cities A and D are caused by burning forests
AThe bigger the population of people living in a city the higher the level of air pollution in that cityBThe land is more polluted in city A than in city CCCity E contains the most pollutants in the airDThe air pollution in cities A and D are caused by burning forests
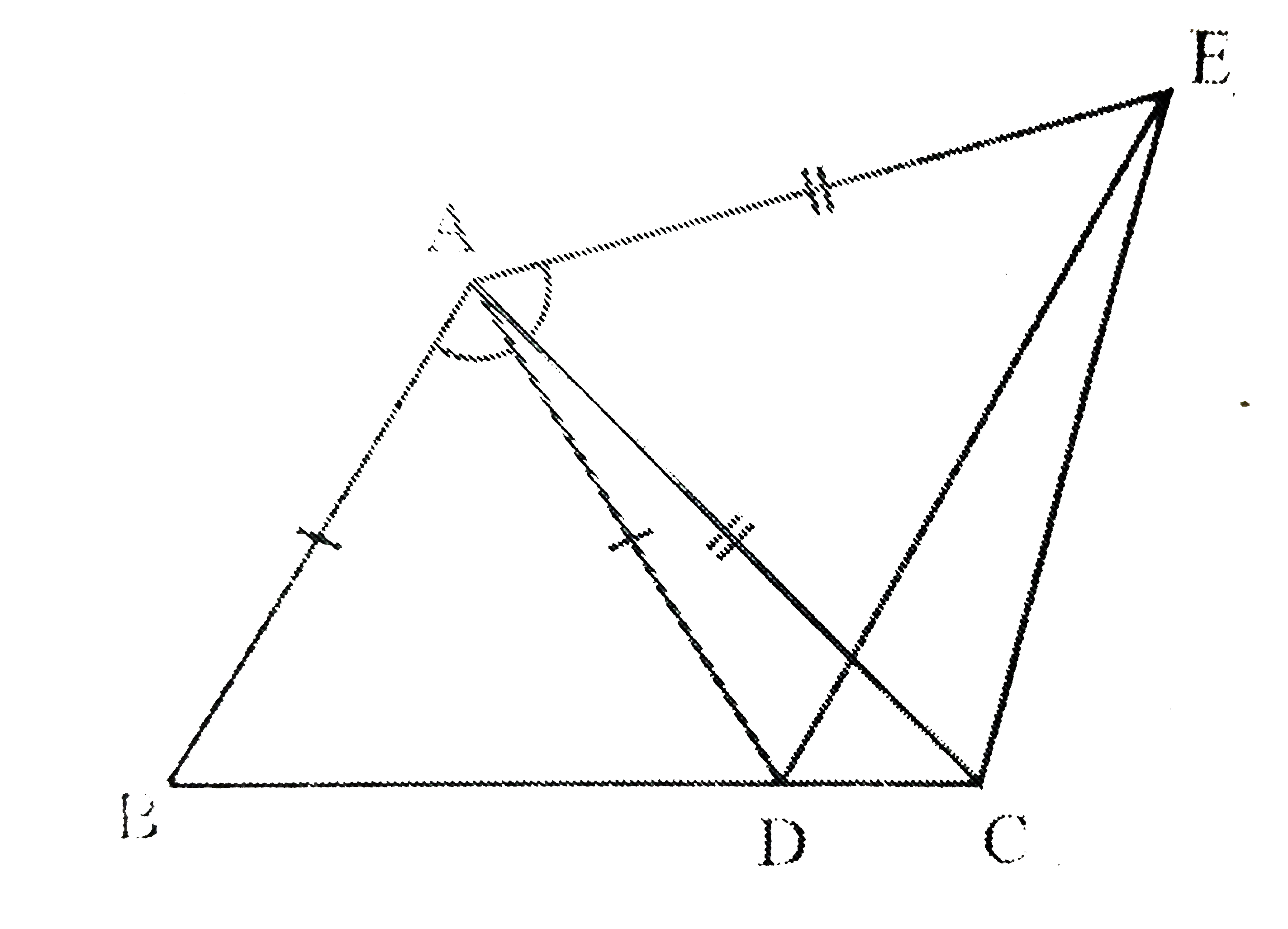
In Fig. 7.21, AC = AE, AB = ADand ∠BAD =∠EAC. Show that BC = DE.
View Solution∠A+∠B+∠C+∠D+∠E=
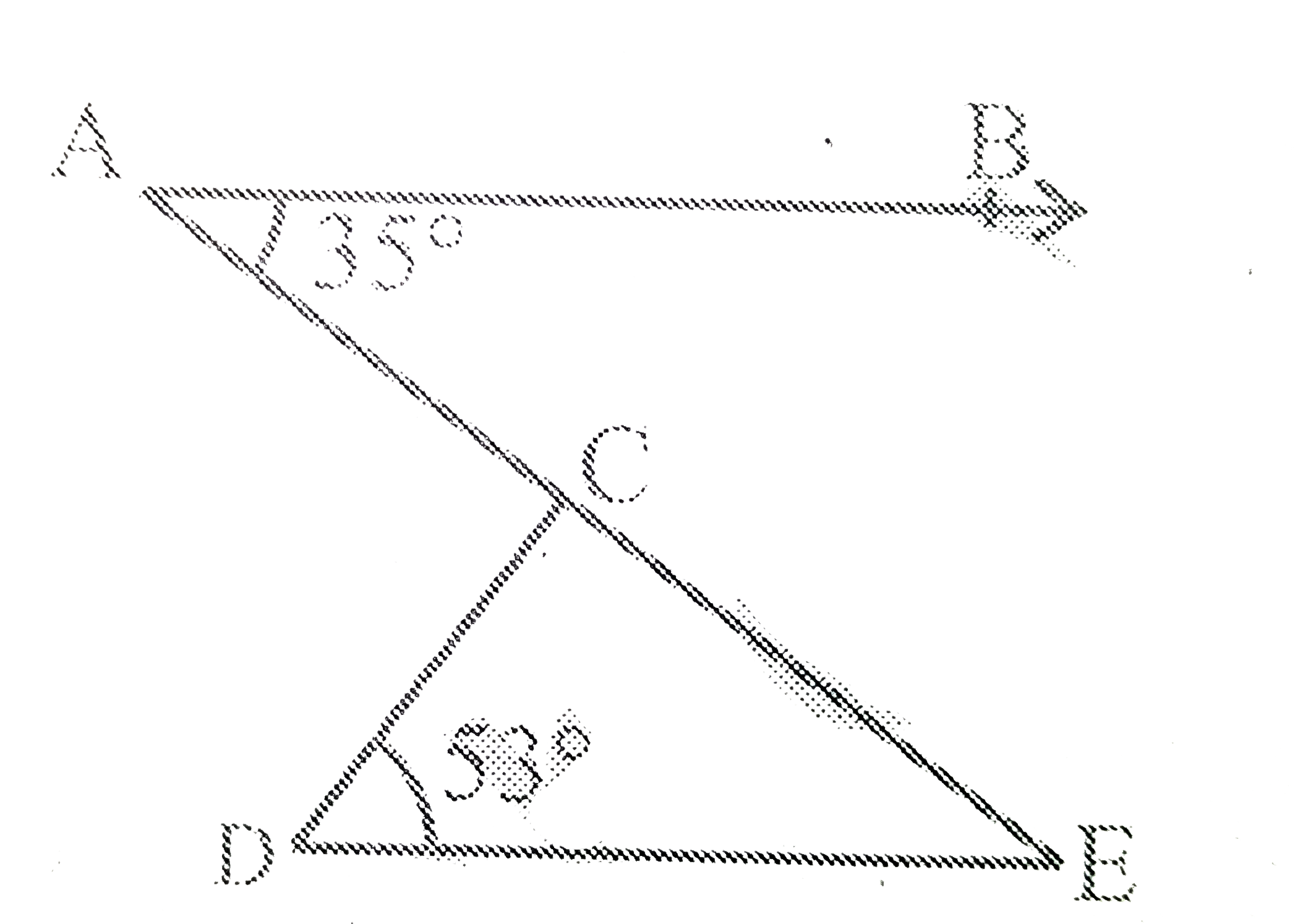
View SolutionIn Fig. 6.41, if AB∣∣DE,∠BAC=35∘ and ∠CDE=53∘, find ∠DCE.
View SolutionIn Fig.87, the corresponding arms of ∠ABC and ∠DEF are parallel. If ∠ABC=750, find the ∠DEF.
View SolutionIn a ABC , D and E are points on the sides AB and AC respectively such that DEBC If AD=6 cm , DB=9 cm and AE=8 cm , find AC . (ii) If ADDB=34 and AC=15 cm , find AE . (iii) If ADDB=23 and AC=18 cm , find AE .
View SolutionIn a ABC , D and E are points on AB and AC respectively such that DE/BC . If AD=2.4cm, AE=3.2cm, DE=2cm and BC=5cm , find BD and CE .
View SolutionIn Fig. 4.101, AD and CE are two altitudes of ABC . Prove that AEF~CDF (ii) ABD~CBE (iii) AEF~ADB (iv) FDC~BEC (FIGURE)
View Solution