What value(s) must be excluded from the domain of f(x)=x+2x−2?
−2
0
2
2 and -2
The correct Answer is:C
To determine the value(s) that must be excluded from the domain of the function f(x)=x+2x−2, we need to analyze the function, particularly the denominator.
1. Identify the Function:
We have the function f(x)=x+2x−2.
2. Determine the Denominator:
The denominator of the function is x−2.
3. Set the Denominator to Zero:
To find the values that must be excluded from the domain, we set the denominator equal to zero:
x−2=0
4. Solve for x:
Solving the equation x−2=0 gives:
x=2
5. Conclusion:
The value x=2 must be excluded from the domain of the function f(x) because it would make the denominator zero, which is undefined in mathematics.
Final Answer:
The value that must be excluded from the domain of f(x) is x=2.
---
We have the function f(x)=x+2x−2.
The denominator of the function is x−2.
To find the values that must be excluded from the domain, we set the denominator equal to zero:
x−2=0
Solving the equation x−2=0 gives:
x=2
The value x=2 must be excluded from the domain of the function f(x) because it would make the denominator zero, which is undefined in mathematics.
The value that must be excluded from the domain of f(x) is x=2.
Topper's Solved these Questions
Similar Questions
If {(3,2),(4,2),(3,1),(7,1),(2,3)} is to be a function, which one of the following must be removed from the set?
05:12View SolutionIf xa⋅(xa+1)a⋅(xa)1−a=xk, then k=
04:57View Solution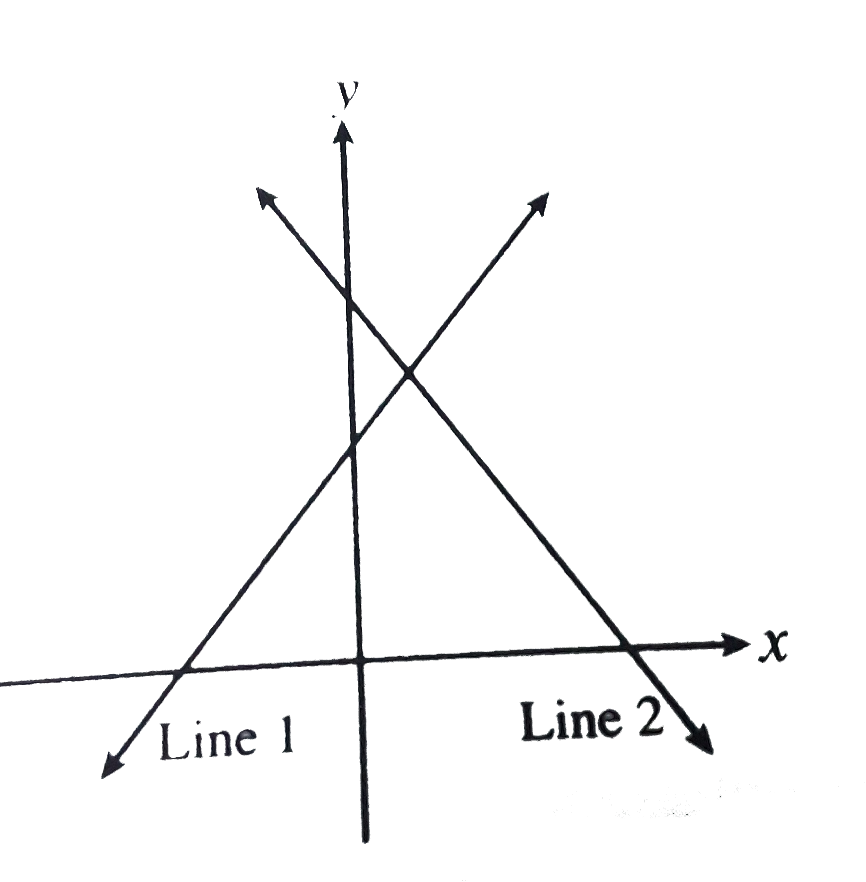
Consider two lines in the xy-plane , as shown above. If line 1 has equation y=m1x+b1, and line 2 has equation y=m2x+b2. Which is a true statement ?02:05View SolutionIf domain of f(x) be (-1,2), then (1) domain of f(sin x) will be (-oo,oo)(2) domain of f(ln x) will be ((1)/(e),e^(2))(3) domain of f(2x-3) will be (1,5/2)(4) domain of f([x]) will be [0,2), where [x]<=x
02:07View SolutionNumber of integral values of x in the domain of f(x)=sqrt(-[x]^(2)+3[x]-2) is
02:03View SolutionIf f(x)=sqrt(log_(x^(2))x, then the domain of f(x) is )
01:54View SolutionThe domain of the real valued function,f(x)=sqrt(5-4x-x^(2))+x^(2)log(x+4) is
04:52View SolutionThe domain of f(x) = x2x2−3x+2 is :
View SolutionFind the domain of the real-valued function:
f(x)=x2−x+1x2−5x+4.01:48View SolutionWhat value must be excluded from the domain of (fg)(x) if f(x)=3x2−4x+1 and g(x)=3x2−3?
03:25View SolutionIf the domain of f(x)=−|x|+2 is −1≤x≤3 f(x) has a minimum value when x equals
01:54View SolutionThe domain of (f(x)=√2+x+√2−xx) is
03:10View SolutionThe domain of the real value function f(x)=√5−4x−x2+x2log(x+4) is ...........
01:13View SolutionConsider the real valued function
f(x)=x−3x2−x−6
Find the domain of f(x).02:13View SolutionThe domain of f(x)=√2+x+√2−xx is
04:19View Solution

