The graph of {x=sin2ty=2cost
straight line
line segment
parabola
portion of a parabola
The correct Answer is:d
To solve the problem of finding the graph of the parametric equations given by x=sin2t and y=2cost, we will eliminate the parameter t to express x in terms of y and identify the resulting curve.
1. Start with the given equations:
x=sin2t
y=2cost
2. Express cost in terms of y:
From the equation for y:
cost=y2
3. Use the Pythagorean identity:
We know that:
sin2t+cos2t=1
Substitute cost from the previous step:
sin2t+(y2)2=1
4. Substitute sin2t with x:
Since x=sin2t, we can substitute:
x+(y2)2=1
5. Simplify the equation:
Expanding the equation gives:
x+y24=1
Rearranging it, we get:
y24=1−x
6. Multiply through by 4 to eliminate the fraction:
y2=4(1−x)
7. Rearranging gives us the standard form of a parabola:
y2=−4x+4
This can be rewritten as:
y2=4(1−x)
8. Identify the characteristics of the parabola:
The equation y2=4(1−x) represents a parabola that opens to the left with its vertex at (1,0).
9. Determine the range of x:
Since x=sin2t, and sin2t varies from 0 to 1, we have:
0≤x≤1
10. Conclusion about the graph:
The graph of the parametric equations is a portion of the parabola y2=4(1−x) that is limited to the values of x from 0 to 1.
x=sin2t
y=2cost
From the equation for y:
cost=y2
We know that:
sin2t+cos2t=1
Substitute cost from the previous step:
sin2t+(y2)2=1
Since x=sin2t, we can substitute:
x+(y2)2=1
Expanding the equation gives:
x+y24=1
Rearranging it, we get:
y24=1−x
y2=4(1−x)
y2=−4x+4
This can be rewritten as:
y2=4(1−x)
The equation y2=4(1−x) represents a parabola that opens to the left with its vertex at (1,0).
Since x=sin2t, and sin2t varies from 0 to 1, we have:
0≤x≤1
The graph of the parametric equations is a portion of the parabola y2=4(1−x) that is limited to the values of x from 0 to 1.
Topper's Solved these Questions
Similar Questions
Knowledge Check
- Question 1 - Select One
In the graph of the parametric equation {x=t2+ty=t2−t
Ax≥0Bx≥−14Cx is any real numberDx≥−1 - Question 2 - Select One
The graph of y=(x+2)(2x-3) can be expressed as a set of parametric equations. If x=2t-2 and y=f(t) , then f(t)=
A2t(4t-5)B(2t-2)(4t-7)C2t(4t-7)D(2t-2)(4t-5)
x=sint,y=cos2t
View SolutionThe graphs of y=sinx,y=cosx,y=tanx&y=cosecx drawn on the same axes from 0→π/2 . A vertical one is drawn through the point where the graph of y=cosx&y=tanx cross, intersecting the other two graphs at the points A&B . The length of the line segment AB is 1 b. √5−12 c. √2 d. √5+12
View SolutionThe graphs of y=sinx,y=cosx,y=tanx&y=cosecx drawn on the same axes from 0⊤i/2 . A vertical one is drawn through the point where the graph of y=cosx&y=tanx cross, intersecting the other two graphs at the points A&B . The length of the line segment AB is 1 b. √5−12 c. √2 d. √5+12
View SolutionFind the equation of tangent to the curve given by x=2sin3t,y=2cos3t at a point where t=π2 ?
View SolutionThe graph of y=cos.x2 is shown in Figure Point a has coordinates (t, 0). What is the value of t in radians ?
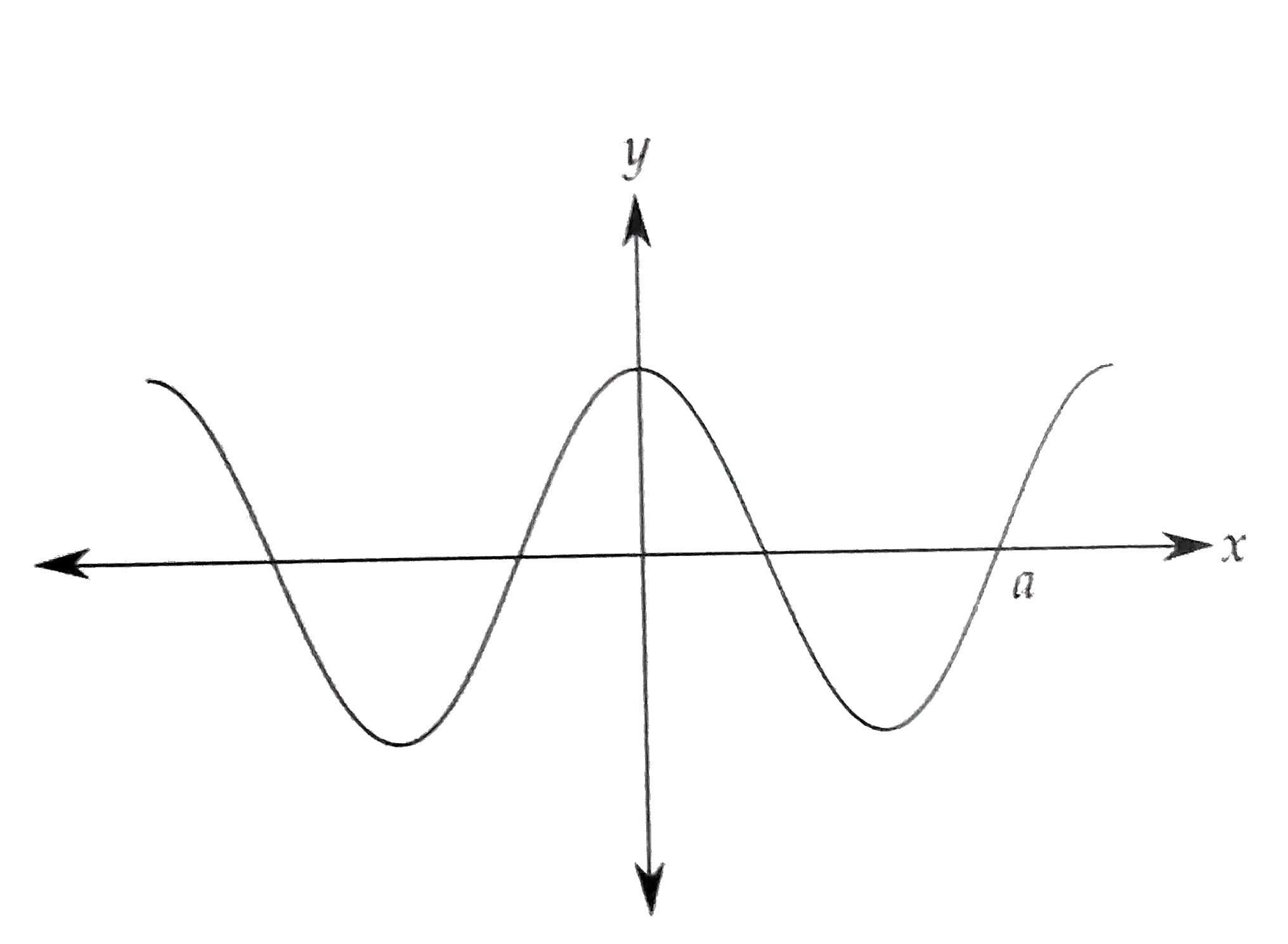 View Solution
View SolutionFind the slope of the normal to the curve x=asin3t,y=bcos3t at point where t=π2.
View Solution

