A mobile phone-based taxi service a base fee of $2 plus an amount per mile for the trip. Ariel is charged $16.94 for a ride that takes 14 minutes and travels 10 miles. Victoria is charged $11.30 for ride that take 10 minutes and travels 6 miles.
Q. What is the per-minute charge?
The correct Answer is:
To solve the problem step by step, we need to establish equations based on the information provided about the taxi service charges.
Step 1: Define Variables
Let:
- X = charge per minute (in dollars)
- Y = charge per mile (in dollars)
Step 2: Set Up Equations
From the information given:
1. Ariel's Charges:
- Total charge = $16.94
- Ride time = 14 minutes
- Distance = 10 miles
The equation for Ariel can be set up as:
16.94=2+14X+10Y
Simplifying this gives:
14X+10Y=16.94−2
14X+10Y=14.94(Equation 1)
2. Victoria's Charges:
- Total charge = $11.30
- Ride time = 10 minutes
- Distance = 6 miles
The equation for Victoria can be set up as:
11.30=2+10X+6Y
Simplifying this gives:
10X+6Y=11.30−2
10X+6Y=9.30(Equation 2)
Step 3: Solve the Equations
Now we have two equations:
1. 14X+10Y=14.94
2. 10X+6Y=9.30
To eliminate Y, we can manipulate these equations. We can multiply Equation 1 by 3 and Equation 2 by 5 to align the coefficients of Y:
- Multiply Equation 1 by 3:
42X+30Y=44.82(Equation 3)
- Multiply Equation 2 by 5:
50X+30Y=46.50(Equation 4)
Step 4: Subtract the Equations
Now, we subtract Equation 3 from Equation 4:
(50X+30Y)−(42X+30Y)=46.50−44.82
This simplifies to:
8X=1.68
Now, solving for X:
X=1.688=0.21
Step 5: Conclusion
The per-minute charge X is $0.21.
Let:
- X = charge per minute (in dollars)
- Y = charge per mile (in dollars)
From the information given:
1. Ariel's Charges:
- Total charge = $16.94
- Ride time = 14 minutes
- Distance = 10 miles
16.94=2+14X+10Y
Simplifying this gives:
14X+10Y=16.94−2
14X+10Y=14.94(Equation 1)
- Total charge = $11.30
- Ride time = 10 minutes
- Distance = 6 miles
11.30=2+10X+6Y
Simplifying this gives:
10X+6Y=11.30−2
10X+6Y=9.30(Equation 2)
Now we have two equations:
1. 14X+10Y=14.94
2. 10X+6Y=9.30
42X+30Y=44.82(Equation 3)
50X+30Y=46.50(Equation 4)
Now, we subtract Equation 3 from Equation 4:
(50X+30Y)−(42X+30Y)=46.50−44.82
This simplifies to:
8X=1.68
Now, solving for X:
X=1.688=0.21
The per-minute charge X is $0.21.
Topper's Solved these Questions
Similar Questions
A mobile phone-based taxi service a base fee of $2 plus an amount per mile for the trip. Ariel is charged $16.94 for a ride that takes 14 minutes and travels 10 miles. Victoria is charged $11.30 for ride that take 10 minutes and travels 6 miles.
Q. What would be the carge for a ride that takes 8 minutes and travels 5 miles?
View SolutionUnited Telephone charges a base rate of $10.00 for service, plus an additional charge of $0.25 per minute. Atlantic Cell charges a base rate of $12.00 for service, plus an additional charge of $0.20 per minute. For what number of minutes would the bills for each telephone company be the same?
View Solution
Knowledge Check
A cyclist travels at 12 miles per hour. How many minutes will it take him to travel 24 miles
A1B120C30D60A phone company charges 10 cents per minute for the first 3 minute of a call and 10 -c cents for each minute thereafter. What is the cost, in cents, of a 10 -minute phonecall?
A100c+70B30+7cC100−7cD100−70cA cyclist travels 20 miles at a second of 15 miles per hours. If he returns along the same path and the entire trip takes 2 hours, at what spped did he return?
A15 mphB20 mphC22 mphD30 mph
United Telephone charges a base rate of $10.00 for service, plus an additional charge of $0.25 per minute. Atlantic Call charges a base rate of $12.00 for service, plus an additional charge of $0.20 per minute. For what number of minutes would the bills for each telephone company be the same?
View Solution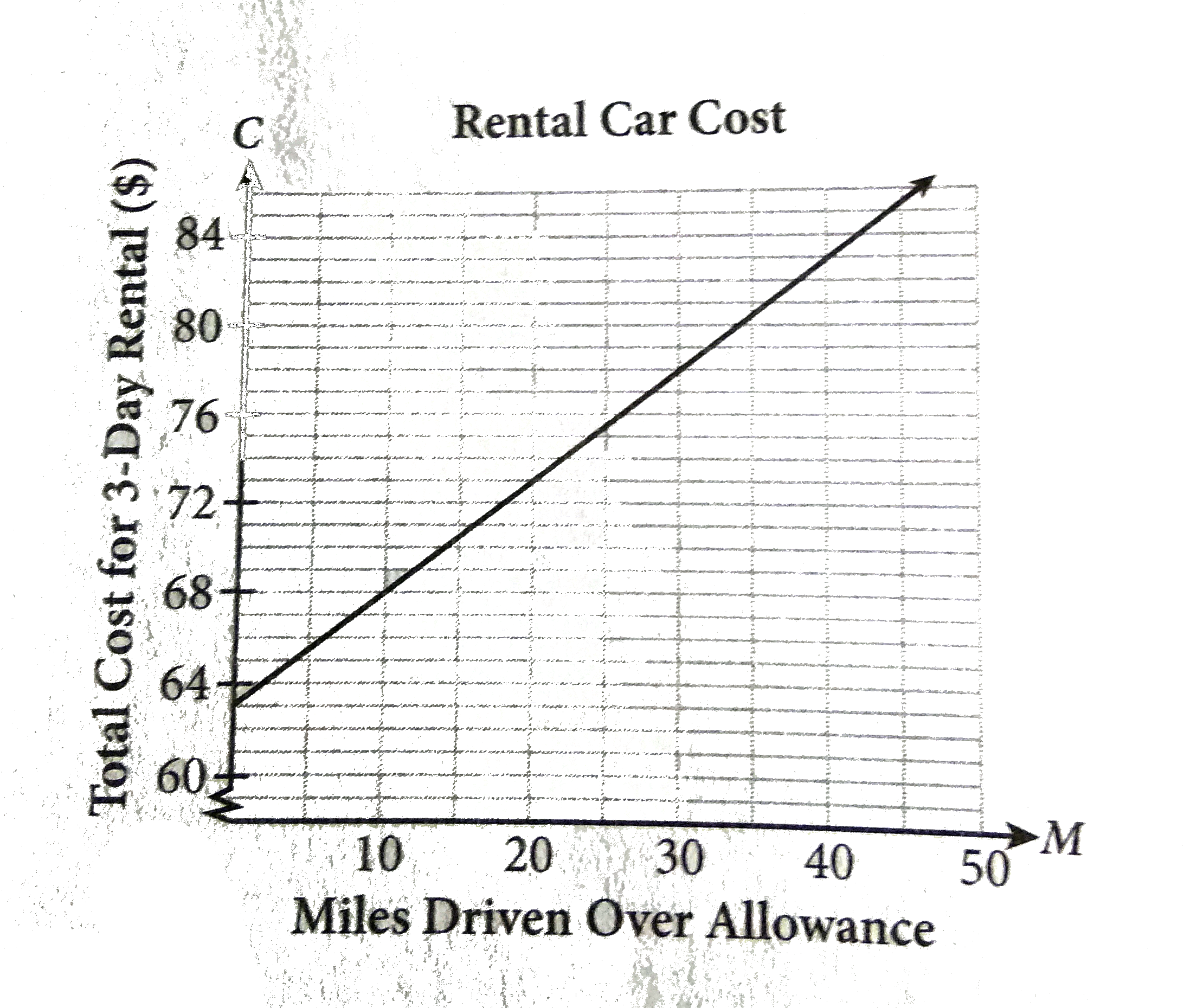
A car retal agency charges a per day rental fee which includes a daily mile age allowance plus a certain amount per mile driven over the allowance. The graph above compares the miles driven over the allowance and the total cost for a 3-day rental. What does the C-intercept most likely represent in this scenario?
View SolutionGary takes a New York City cab 6 miles to work and must pay $17.50 for the cab ride. After work, Gary takes another New York City cab 10 miles to visit his family and must pay $27.50. During both of these rides, Gary was charged a ''drop fee'' (an initial charge when the cab's meter is activated) of dollars, plus an additional m dollars for each 15 of a mile travelled. What is the value of md?
View SolutionPaula jogged for a total of 30 minutes. Her average speed for the first 10 minutes was 5 miles per hour. During the remainder of her time, she jogged 2.5 miles. What was Paula's average for her entire jog ?
View SolutionWaugh jogged to a restaurent at x miles per hour, and jogged back home along the same route at y miles per hour. He took 30 minutes for the whole trip. If the restaurant is 2 miles form home along the route he too, what is the average speed in miles per hour at which he jogged for the whole trip ?
View Solution
