A ring of radius R is rolling purely on the outer surface of a pipe of radius 4R At some instant the center of the ring has constant speed =v then the acceleration of the point on the ring which is in contact with the surface of the pipe is
4v2/5R
3v2/5R
v2/4R
zero
The correct Answer is:A
To find the acceleration of the point on the ring that is in contact with the surface of the pipe, we can follow these steps:
Step 1: Identify the parameters
- The radius of the ring is R.
- The radius of the pipe is 4R.
- The center of the ring is moving with a constant speed v.
Step 2: Determine the distance from the center of the ring to the center of the pipe
The distance from the center of the ring to the center of the pipe is:
Distance=R+4R=5R
Step 3: Calculate the centripetal acceleration of the center of the ring
The centripetal acceleration acm of the center of the ring is given by the formula:
acm=v2r
where r is the radius of the circular path, which in this case is 5R:
acm=v25R
Step 4: Determine the angular velocity ω
Since the ring is rolling without slipping, we can relate the linear speed v to the angular speed ω using the formula:
v=ωR
Thus, we can express ω as:
ω=vR
Step 5: Calculate the centripetal acceleration of the point in contact with the pipe
The point in contact with the pipe also experiences centripetal acceleration due to its circular motion around the center of the ring. This acceleration an is given by:
an=ω2r
where r is the radius of the ring R:
an=(vR)2R=v2R
Step 6: Determine the net acceleration of the point in contact
The net acceleration a of the point in contact with the pipe is the difference between the centripetal acceleration of the center of the ring and the centripetal acceleration of the point in contact:
a=acm−an
Substituting the values we calculated:
a=v25R−v2R
To combine these fractions, we find a common denominator:
a=v25R−5v25R=v2−5v25R=−4v25R
Final Result
The acceleration of the point on the ring which is in contact with the surface of the pipe is:
a=−4v25R
- The radius of the ring is R.
- The radius of the pipe is 4R.
- The center of the ring is moving with a constant speed v.
The distance from the center of the ring to the center of the pipe is:
Distance=R+4R=5R
The centripetal acceleration acm of the center of the ring is given by the formula:
acm=v2r
where r is the radius of the circular path, which in this case is 5R:
acm=v25R
Since the ring is rolling without slipping, we can relate the linear speed v to the angular speed ω using the formula:
v=ωR
Thus, we can express ω as:
ω=vR
The point in contact with the pipe also experiences centripetal acceleration due to its circular motion around the center of the ring. This acceleration an is given by:
an=ω2r
where r is the radius of the ring R:
an=(vR)2R=v2R
The net acceleration a of the point in contact with the pipe is the difference between the centripetal acceleration of the center of the ring and the centripetal acceleration of the point in contact:
a=acm−an
Substituting the values we calculated:
a=v25R−v2R
To combine these fractions, we find a common denominator:
a=v25R−5v25R=v2−5v25R=−4v25R
The acceleration of the point on the ring which is in contact with the surface of the pipe is:
a=−4v25R
Topper's Solved these Questions
- BOOK - BANSALCHAPTER - MASTER PRACTICE PROBLEMEXERCISE - Comphrehension134videos
MASTER PRACTICE PROBLEM
- BOOK - BANSALCHAPTER - MASTER PRACTICE PROBLEMEXERCISE - Reasoning75videos
MASTER PRACTICE PROBLEM
- BOOK - BANSALCHAPTER - FLUID MECHANICSEXERCISE - PYQS AIEEE10videos
FLUID MECHANICS
- BOOK - BANSALCHAPTER - SEMICONDUCTORSEXERCISE - CBSE Question32videos
SEMICONDUCTORS
Similar Questions
A convex surface has a uniform radius of curvature equal to 5R. A wheel of radius R is rolling without sliding on it with a constant speed v. Find the acceleration of the point (P) of the wheel which is in contact with the convex surface.
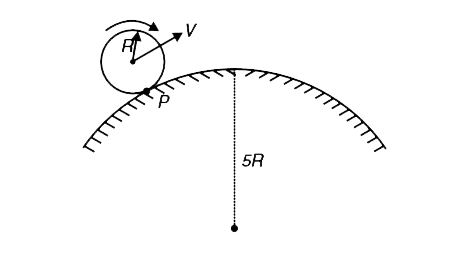 View Solution
View SolutionA thin ring of mass m and radius R is in pure rolling over a horizontal surface. If v0 is the velocity of the centre of mass of the ring, then the angular momentum of the ring about the point of contact is
View Solution
Knowledge Check
- Question 1 - Select One

A disc of radius R is rolling purely on a flat horizontal surface, with a constant angular velocity the angle between the velocity ad acceleration vectors of point P isAzeroB45∘Ctan−1(2)Dtan−1(1/2) - Question 2 - Select One
A disc of radius R is rolling purely on a flat horizontal surface, with a constant angular velocity. The angle between the velocity and acceleration vectors of point P is
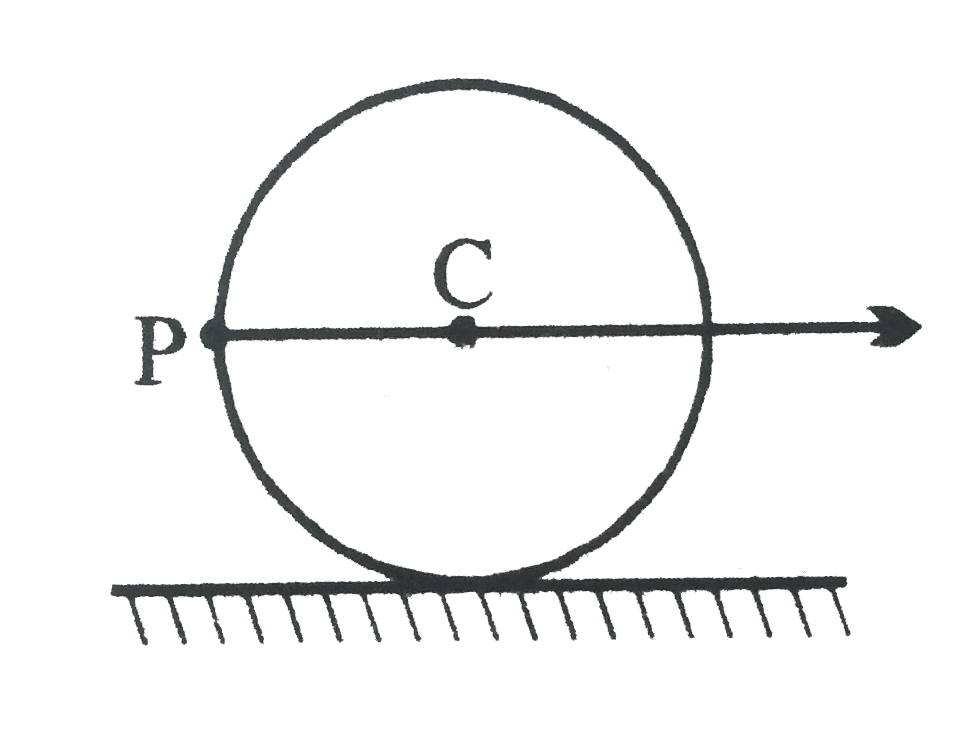 .AzeroB45∘C135∘Dtan−1(1/2)
.AzeroB45∘C135∘Dtan−1(1/2) - Question 3 - Select One or More
A ring of radius r is moving without slipping on a circular track of radius R speed of the centre of the ring is v=ωr. Ignoring the fact that the ring axis is inclined
 AThe radial acceleration of centre of the ring is ω2r2RBThe radial acceleration of centre of the ring is (R−r)2Rω2CThe angular velocity of centre of the ring about vertical axis passing through the centre of track is rω/R.DThe angular velocity of centre of the ring about vertical axis passing through the centre of track is (R−r)Rω
AThe radial acceleration of centre of the ring is ω2r2RBThe radial acceleration of centre of the ring is (R−r)2Rω2CThe angular velocity of centre of the ring about vertical axis passing through the centre of track is rω/R.DThe angular velocity of centre of the ring about vertical axis passing through the centre of track is (R−r)Rω
In case of pure rolling, what will be the velocity of point A of the ring of radius R?
 View Solution
View SolutionA ring of radius R has charge −Q distributed uniformly over it. Calculate the charge that should be placed at the center of the ring such that the electric field becomes zero at apoint on the axis of the ring at distant R from the center of the ring.
View SolutionPotential on the axis of ring of radius 3R and at distance 4R from centre of ring is (charge on the ring is Q )
View Solution
A ring of radius R rolls on a horizontal surface with constant acceleration a of the centre of mass as shown in figure. If ω is the instantaneous angular velocity of the ring. Then the net acceleration of the point of contact of the ring with gound isView SolutionA ring performs pure rolling on a horizontal surface and its state at some instant of time is shown in figure.
 View Solution
View Solution

