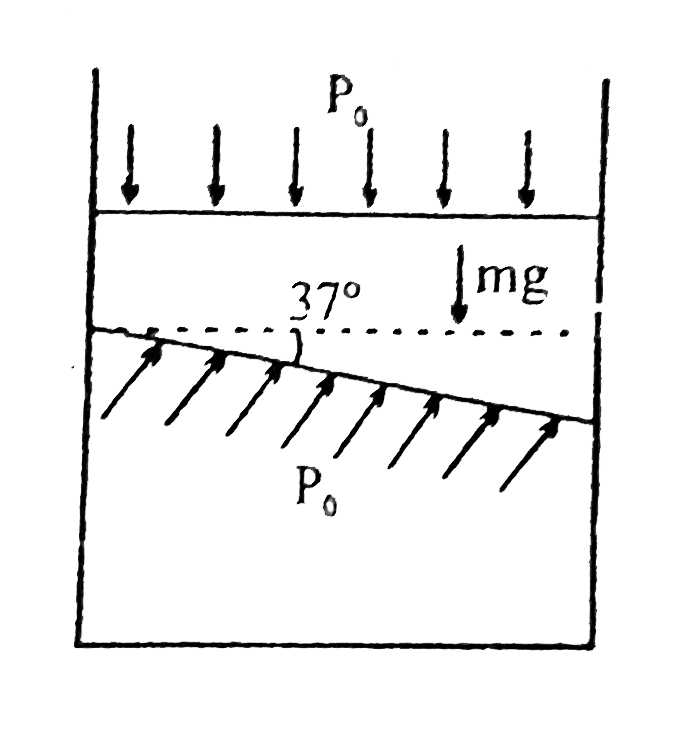
In the cylinder shown in the figure, air is enclosed under the piston. Piston mass M=60 kg, crosssectional area of the cylinder S0=20cm2 atmospheric pressure P0=105paα=37∘. The air temperature is constant, the friction is negligible.

What is the pressure of the enclosed gas?
3.4×105 Pa
4×105 Pa
4.75×105 Pa
2.8×105 Pa
The correct Answer is:B
P0×S0+mg=P×S0sec37∘×cos37∘
⇒P=P0+mgS0
⇒105+60020×10−4
=4×105 Pa
Topper's Solved these Questions
- MASTER PRACTICE PROBLEMBOOK - BANSALCHAPTER - MASTER PRACTICE PROBLEMEXERCISE - Reasoning
75 Videos
- MASTER PRACTICE PROBLEMBOOK - BANSALCHAPTER - MASTER PRACTICE PROBLEMEXERCISE - Multiple objective
131 Videos
- MASTER PRACTICE PROBLEMBOOK - BANSALCHAPTER - MASTER PRACTICE PROBLEMEXERCISE - Additional topic
70 Videos
- FLUID MECHANICSBOOK - BANSALCHAPTER - FLUID MECHANICSEXERCISE - PYQS AIEEE
10 Videos
- SEMICONDUCTORSBOOK - BANSALCHAPTER - SEMICONDUCTORSEXERCISE - CBSE Question
32 Videos
Similar Questions
A cylinderical vessel contaning liquid is closed by a smooth piston of mass m. the area of cross-section of the piston is A. if the atmospheric pressure is P0, Find the pressure of the liquid just below the piston.
View SolutionA cylindrical vessel containing a liquid is closed by a smooth piston of mass "100g" as shown in the figure.The radius of the piston is "10cm" .If the atmospheric pressure is P0 then the pressure difference of the liquid just below the piston and the atmospheric pressure is (g=10ms2)
View Solution
Knowledge Check
In the cylinder shown in the figure, air is enclosed under the piston. Piston mass M=60 kg, crosssectional area of the cylinder S0=20cm2 atmospheric pressure P0=105paα=37∘. The air temperature is constant, the friction is negligible.

What is the mass of the goods that must be put on the piston so that the volume of the gas becomes half?A56kgB80kgC110 kgD92 kgA non - conducting piston of mass m and are S0 divides a non - conducting, closed cylinder as shown in the figure. A piston having mass m is connected with the top wall of the cylinder by a spring of force constant k. The top part is evacuated and the bottom part is evacuated and the bottom part contains an ideal gas at a pressure P0 in the equilibrium position. Adiabatic exponent γ and in equilibrium length of each part is l. (neglect friction). Find the angular frequency for small oscillation.
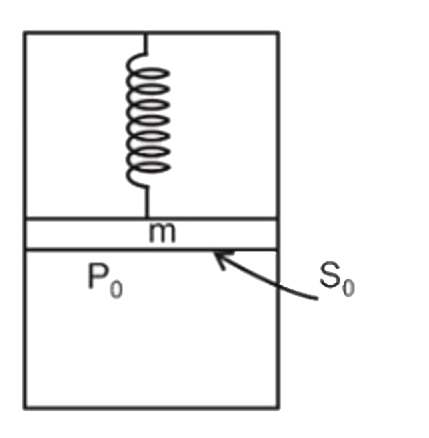 A√kl+γP0S02mlB√3kl+γP0S0mlC√kmD√kl+γP0S0ml
A√kl+γP0S02mlB√3kl+γP0S0mlC√kmD√kl+γP0S0mlIn the arrangement shown in Fig. gas is thermally insulated. An ideal gas is filled in the cylinder having pressure P0 (gt atmospheric pressure P0). The spring of force constant K is initially unstretched. The piston of mass m and area S is frictionless. In equilibrium, the piston rises up by distance x0, then
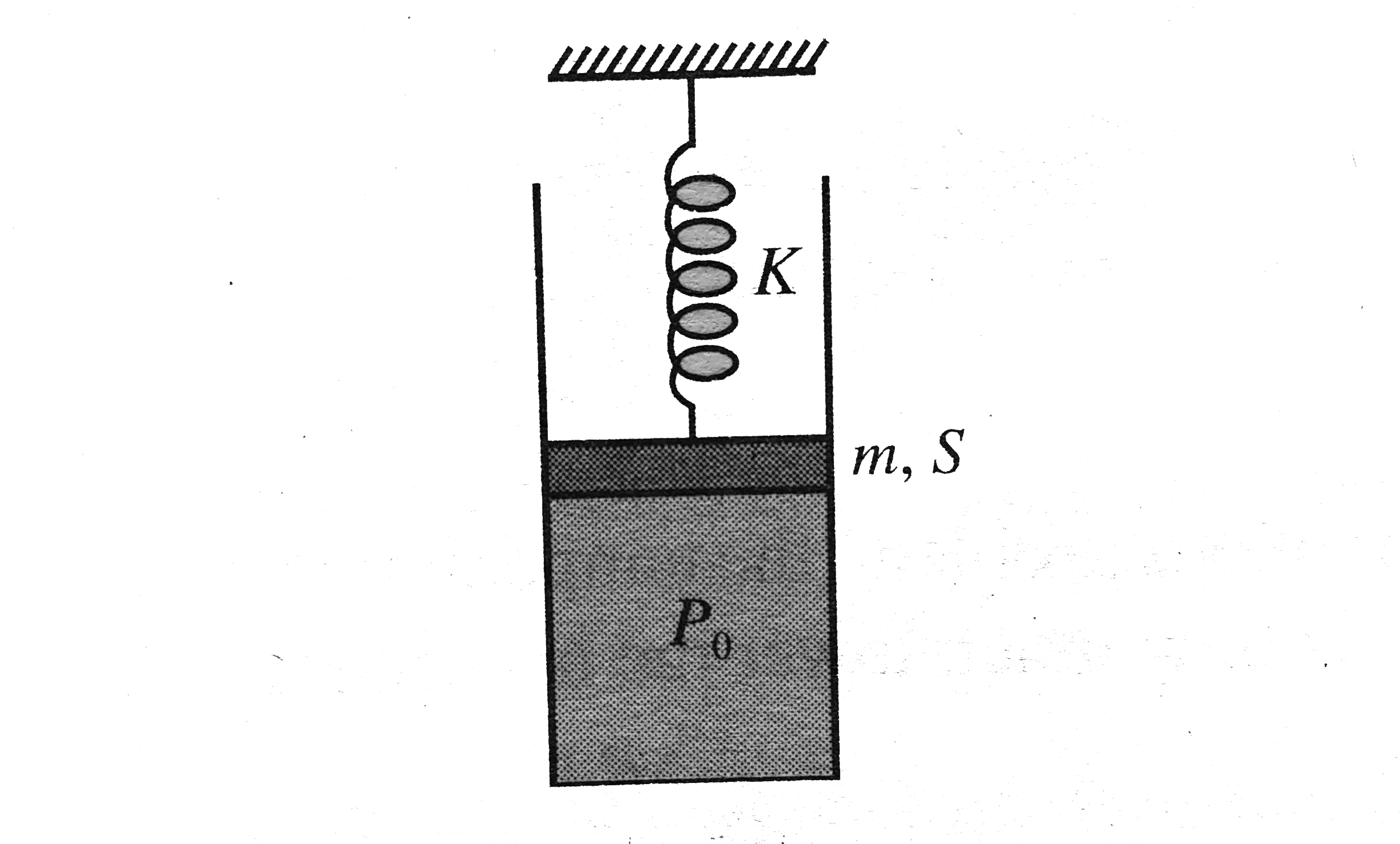 Afinal pressure of the gas is P0+Kx0S+mgSBwork done by the gas is 12Kx20+mgx0Cdecrease in internal energy of the gas is 12Kx20+mgx0+P0Sx0Dall of the above
Afinal pressure of the gas is P0+Kx0S+mgSBwork done by the gas is 12Kx20+mgx0Cdecrease in internal energy of the gas is 12Kx20+mgx0+P0Sx0Dall of the above
A cylidrical vesel containing a liquid is closed by a smooth piston of mass m as shown in the figure. The area of cross section of the piston is A. If the atmospheric pressure is P0, find the pressure of the liquid just below the piston.
 ,
,
View SolutionA cylinder fitted with a spring loaded piston, shown in the figure, contains 0.01(m)3 gas at a pressure of 105Pa. The cross-sectional area of the piston is 0.05m2. Initially, the spring does not touch the piston but atmospheric pressure of 105Pa acts on the piston. The gas is slowly heated till the volume is increased to three times the original value. If the forcé constant of the spring is 25kNm, calculate the work done (in kJ ) by the gas.
'(##CEN_KSR_PHY_JEE_C15_E01_031_Q19##)'
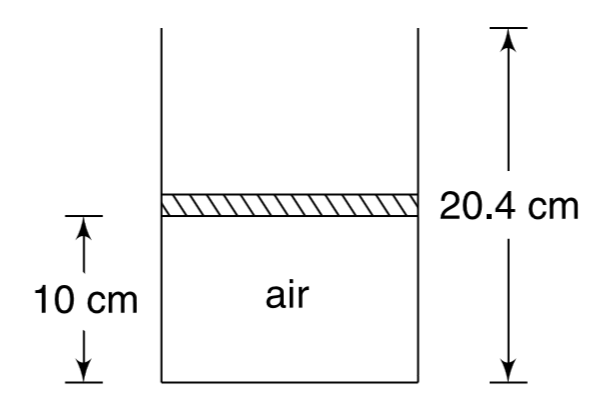
View SolutionIn the arrangement shown in figure, the piston can smoothly move inside the cylinder. The mass of the piston is m = 100 g and its cross sectional area is A=10cm2. The length of air column at temperature of T=27∘C is 10 cm. Overall length of the cylinder is 20.4 cm. The container is turned upside down and the length of the air column in equilibrium was found to be l at 27∘C. Take R=253Jmol−1K−1 and assume air to be diatomic gas. g=10m/s2, atmospheric pressure is 1.01×105Nm2
(a) Find l
(b) If the air in the container is supplied heat in upside down position, the piston slowly begins to move down, and ultimately it gets ejected out of the cylinder. Calculate the amount of heat that the air must absorb for the piston to come out.
View SolutionThe fixed non-conducting cylinder shown in figure has a noconducting heavy piston of mass M that can slide without friction. The area of piston is S and the cylinder is filled with an ideal gas (λ=1.5) with an initial volume V and an initial pressure P. Assume that the outside pressure on the piston is zero (vaccum). (Neglect acceleration due to gravity).
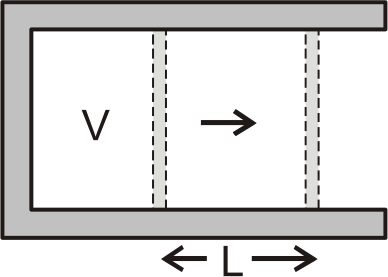
For the temperature of the gas to drop to one half of its original value. the piston will have to move by a distance:
View SolutionA closed and isolated cylinder contains ideal gas. An adiabatic separator of mass m, cross sectional area A divides the cylinder into two equal parts each with volume V0 and pressure P0 in equilibrium Assume the sepatator to move without friction.
If the piston is slightly displaced by x, the net force acting on the piston is
View Solution
