A particle of mass 1kg is projected at an angle of θ=π/4 from horizontal with a muzzle velocity of 20m/s. A long slender rod of mass 5kg and length 30m is suspended vertically from a point at the same horizontal leves as that of point of projection and at a distance of 60m from the projection point. The rod can rotate freely. If collision occurs, it is perfectly plastic. (g=10m/s2)
If projectile is fired horizontally, it will
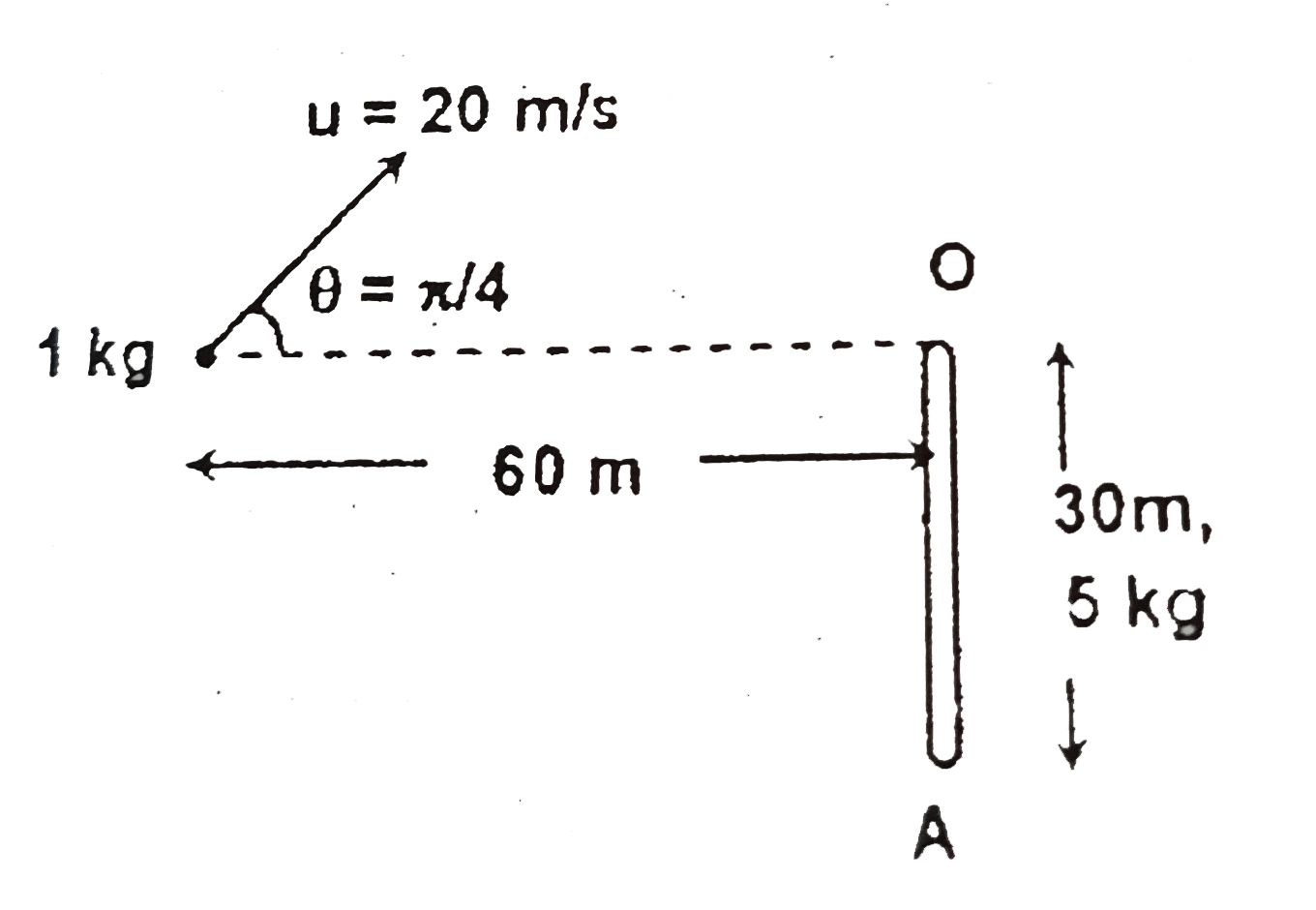
hit the rod between O and A (except mid point)
hit the rod at its mid point
hit the rod at A
not hit the rod at all
Hint : First find the point where collision occurs using equation of trajectory. Then use conservation of angular momentum. After collision energy conservation is valid.
Topper's Solved these Questions
- GMP ASSESMENTBOOK - FIITJEECHAPTER - GMP ASSESMENTEXERCISE - Numerical Based
61 Videos
- GMP ASSESMENTBOOK - FIITJEECHAPTER - GMP ASSESMENTEXERCISE - Multiple Question
58 Videos
- GENERAL PHYSICSBOOK - FIITJEECHAPTER - GENERAL PHYSICSEXERCISE - MATRIX MATCH TYPE
3 Videos
- GRAVITATIONBOOK - FIITJEECHAPTER - GRAVITATIONEXERCISE - Numerical based Question
2 Videos
Similar Questions
A particle of mass 1kg is projected at an angle of θ=π/4 from horizontal with a muzzle velocity of 20m/s. A long slender rod of mass 5kg and length 30m is suspended vertically from a point at the same horizontal leves as that of point of projection and at a distance of 60m from the projection point. The rod can rotate freely. If collision occurs, it is perfectly plastic. (g=10m/s2)
Angular velocity of rod after collision is
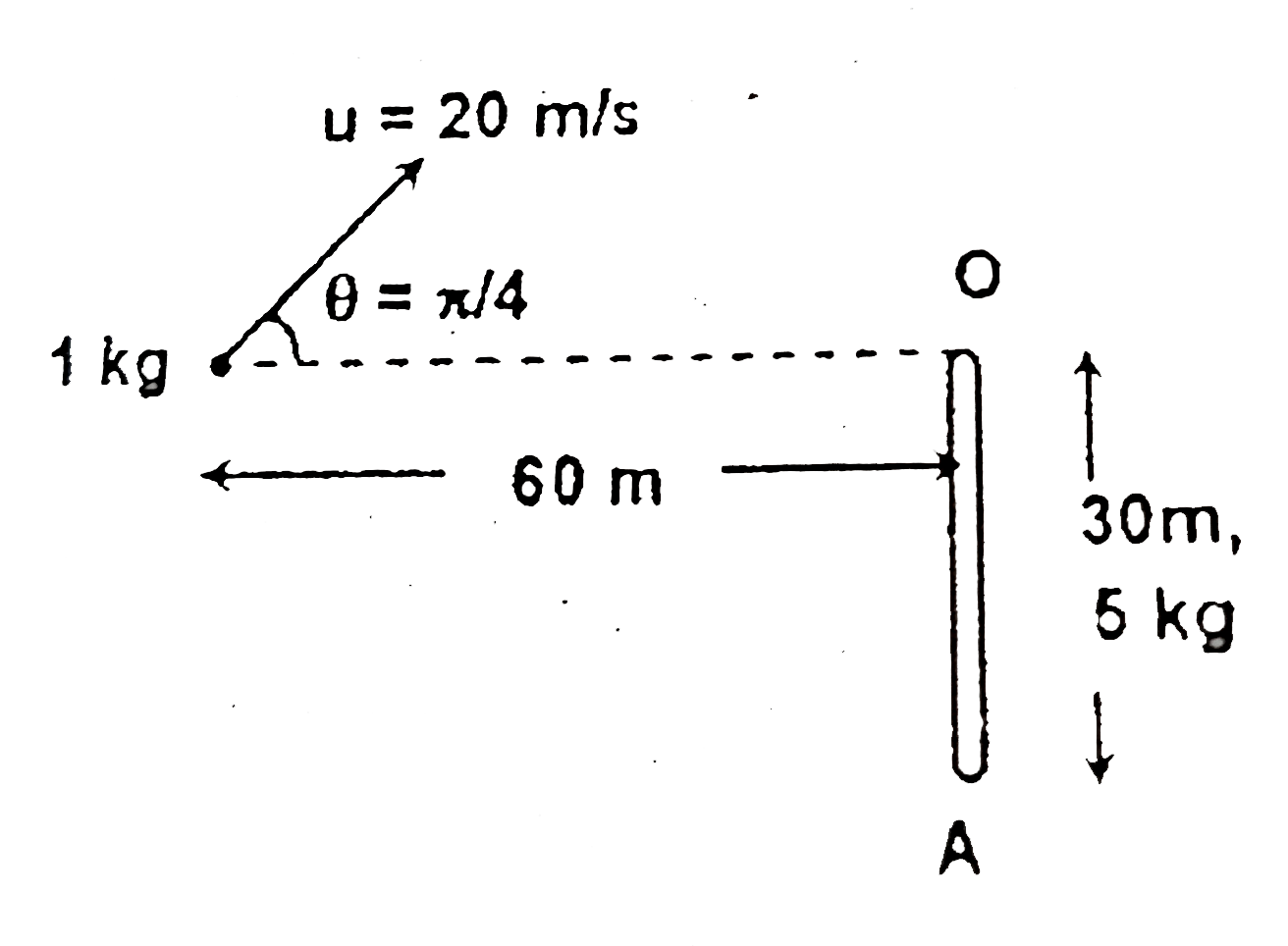
View SolutionA particle of mass 1kg is projected at an angle of θ=π/4 from horizontal with a muzzle velocity of 20m/s. A long slender rod of mass 5kg and length 30m is suspended vertically from a point at the same horizontal leves as that of point of projection and at a distance of 60m from the projection point. The rod can rotate freely. If collision occurs, it is perfectly plastic. (g=10m/s2)
If the rod tilts to an angle θ after collision, then
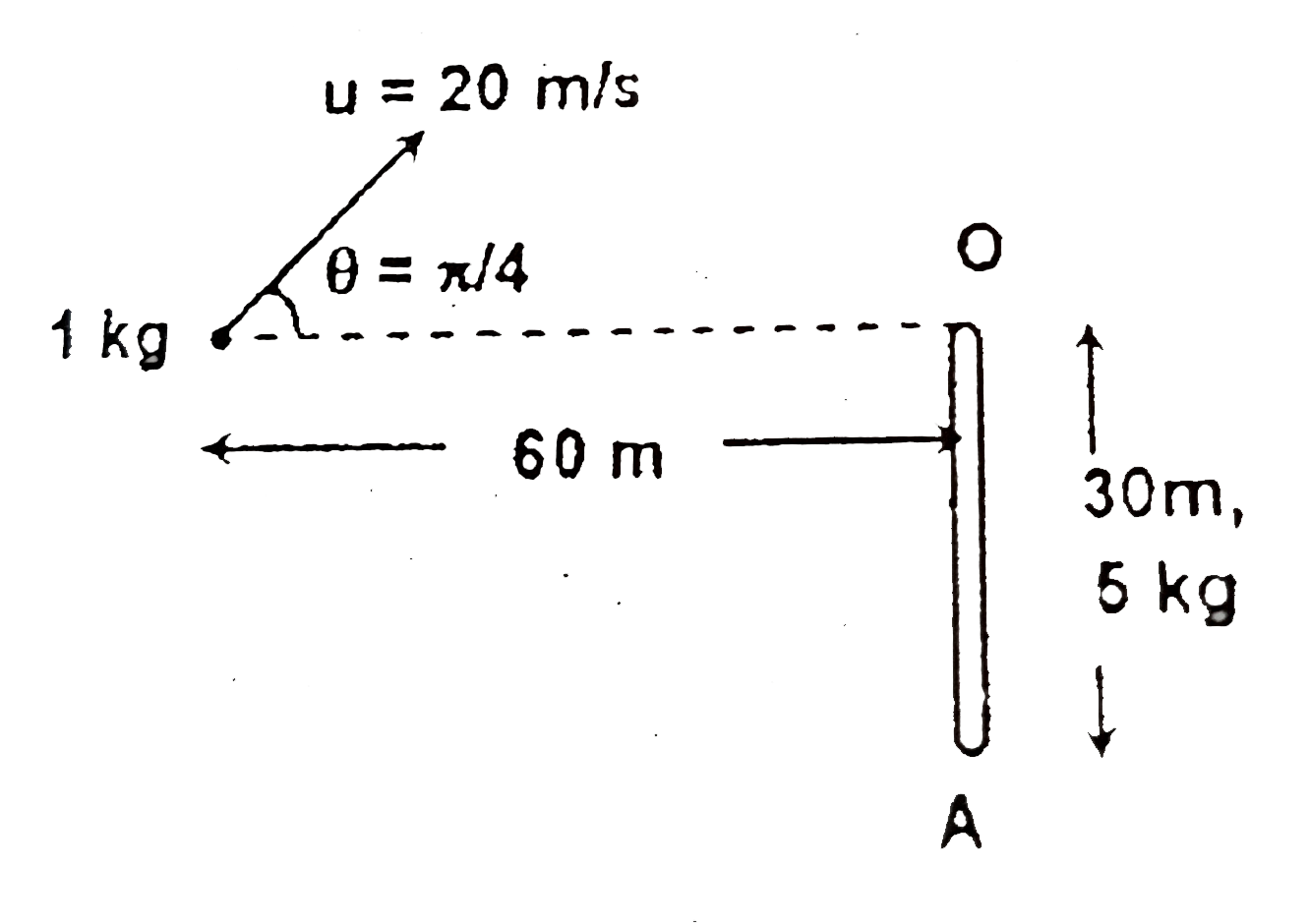
View Solution
Knowledge Check
A particle of mass 1kg is projected at an angle of θ=π/4 from horizontal with a muzzle velocity of 20m/s. A long slender rod of mass 5kg and length 30m is suspended vertically from a point at the same horizontal leves as that of point of projection and at a distance of 60m from the projection point. The rod can rotate freely. If collision occurs, it is perfectly plastic. (g=10m/s2)
Angular velocity of rod after collision is
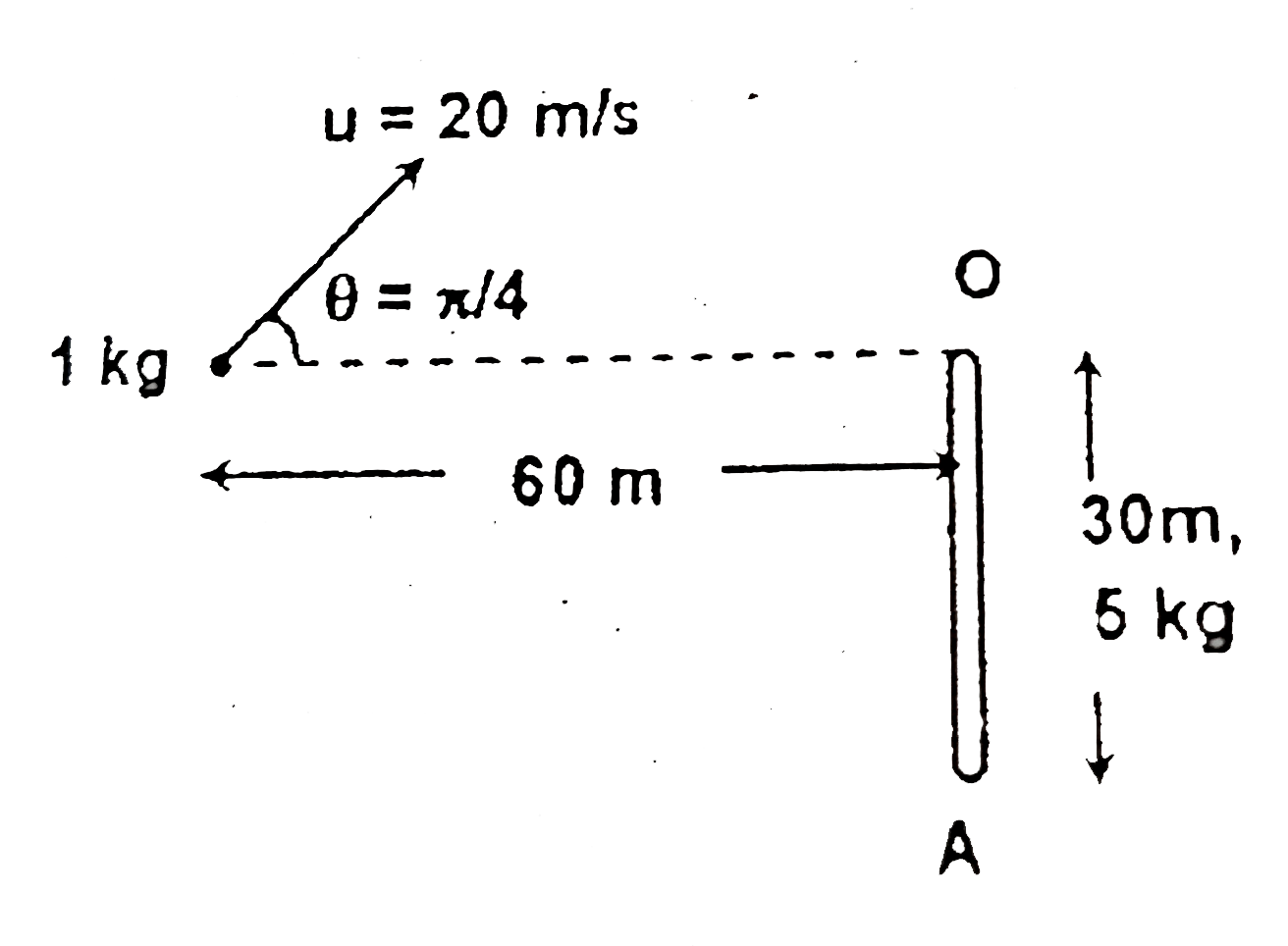 A14√2rad/secB4√2rad/secC4√2rad/secDzero
A14√2rad/secB4√2rad/secC4√2rad/secDzeroA particle of mass 1kg is projected at an angle of θ=π/4 from horizontal with a muzzle velocity of 20m/s. A long slender rod of mass 5kg and length 30m is suspended vertically from a point at the same horizontal leves as that of point of projection and at a distance of 60m from the projection point. The rod can rotate freely. If collision occurs, it is perfectly plastic. (g=10m/s2)
If the rod tilts to an angle θ after collision, then
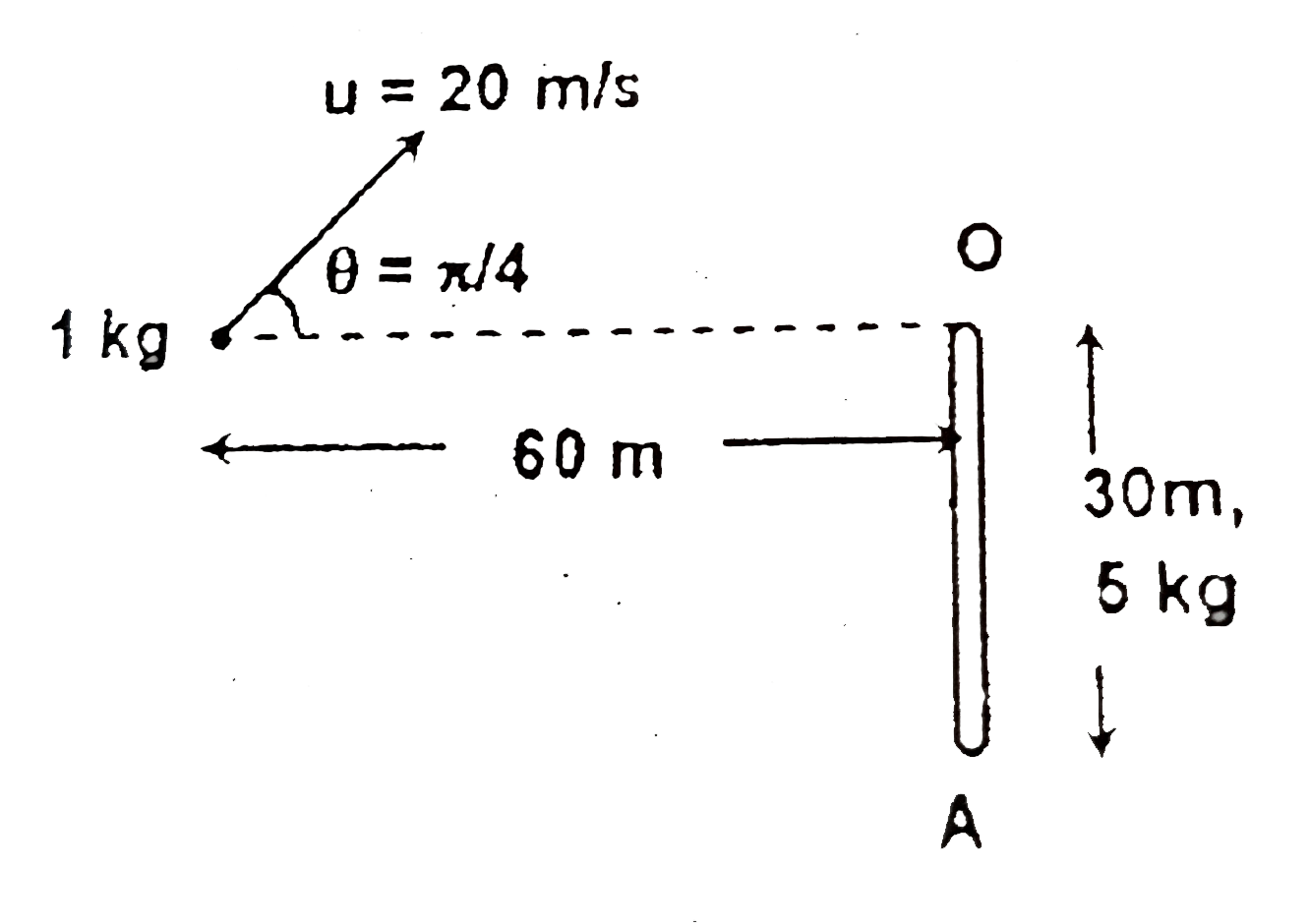 Aθ=0∘Bθ=cos−1(40/42)Cθ=cos−1(41/42)Dθ=cos−1(27/28)
Aθ=0∘Bθ=cos−1(40/42)Cθ=cos−1(41/42)Dθ=cos−1(27/28)A particle is projected with velocity v at an angle of θ with horizontal. The average angular velocity of the particle from the point of projection to impact equals:
AgcosθθvBgvsinθCgvθDgθvsinθ
A projectile of mass 1kg is projected with a velocity of √20m/s such that it strikes on the same level as the point of projection at a distance of √3m. Which of the following options are incorrect:
View SolutionA Iong slender rod of mass 2kg and length m is placed on a smooth horizontal table. Two particles of masses 2kg and 1kg strike the rod simultaneously and stick to the rod after collision as shown in fig.
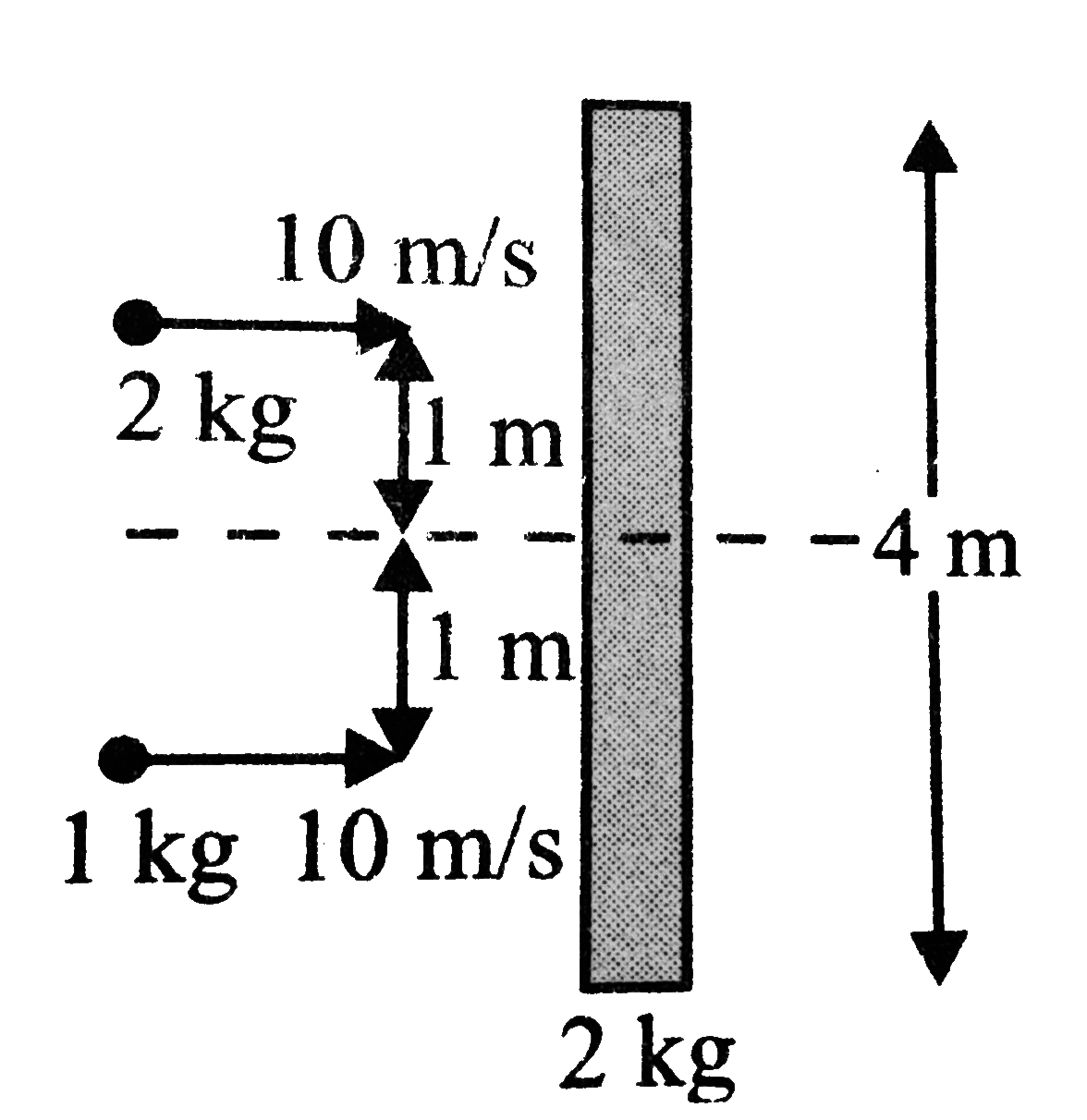
Angular velocity of the rod after collision is
View SolutionA particle of mass m is projected with a speed u at an angle θ with the horizontal. Find angular momentum of particle after time t about point of projection.
View SolutionA Iong slender rod of mass 2kg and length m is placed on a smooth horizontal table. Two particles of masses 2kg and 1kg strike the rod simultaneously and stick to the rod after collision as shown in fig.

Angular velocity of the rod after collision is
View SolutionA particle of mass m is projected with an initial velocity U at an angle θ to the horizontal. The torque of gravity on projectile at maximum height about the point of projection is
View Solution
