The potential energy function for the force between two in a diatomic molecule can approximately be expressed as U(x)=ax12−bx4, where a and b are positive constants, and x is the distance between the atoms. Answer the following question by selecting most appropriate alternative.
The graph between force between the atoms [F(x)] vs x will be
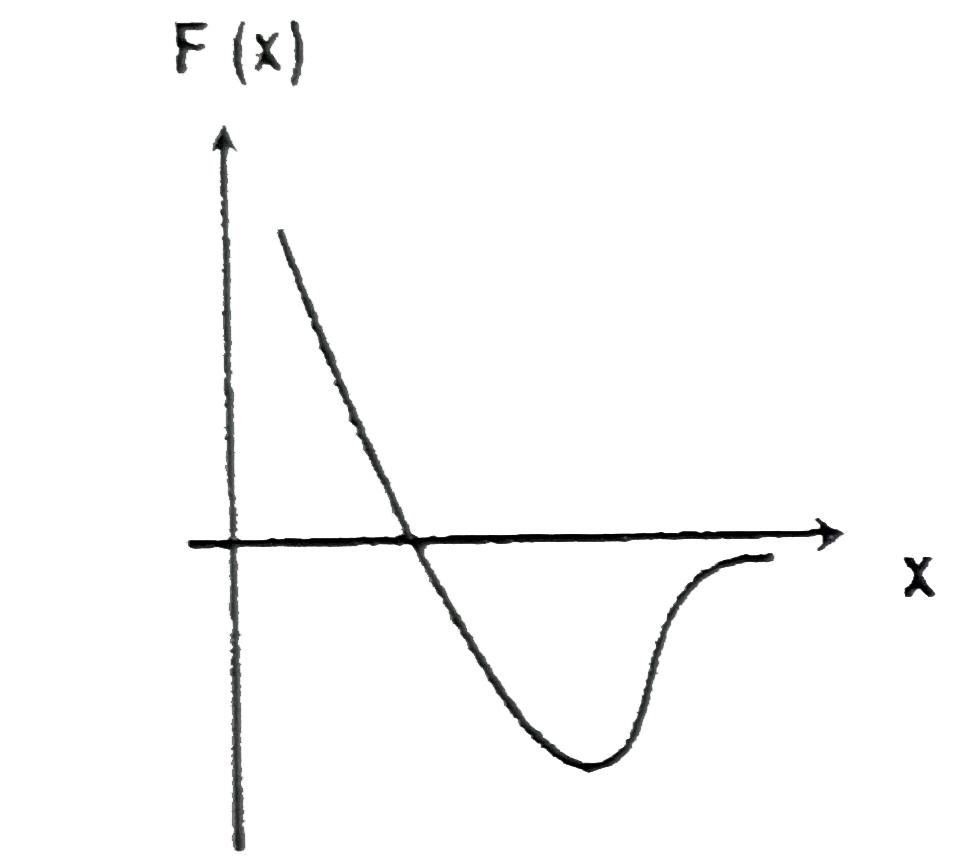
Step by step video & image solution for The potential energy function for the force between two in a diatomic molecule can approximately be expressed as U(x)=(a)/(x^(12))-(b)/(x^(4)), where a and b are positive constants, and x is the distance between the atoms. Answer the following question by selecting most appropriate alternative. The graph between force between the atoms [F(x)] vs x will be by Physics experts to help you in doubts & scoring excellent marks in Class 11 exams.
Updated on:21/07/2023Topper's Solved these Questions
Similar Questions
The potential energy function for the force between two in a diatomic molecule can approximately be expressed as U(x)=ax12−bx4, where a and b are positive constants, and x is the distance between the atoms. Answer the following question by selecting most appropriate alternative.
The graph between potential energy vs x will be
View SolutionThe potential energy function for the force between two in a diatomic molecule can approximately be expressed as U(x)=ax12−bx4, where a and b are positive constants, and x is the distance between the atoms. Answer the following question by selecting most appropriate alternative.
The dissociation energy of the molecule is (initially molecule is at rest at equilibrium)
View Solution
Knowledge Check
The potential energy between two atoms in a molecule is given by U(x)=1x12−(b)x6, where a and b are positive constants and x is the distance between the atoms. The atom is in stable equilibirum when
Ax=6√11a5bBx=6√a2bCx=0Dx=6√2abThe potential energy funtions for the force between two along in a distance molecule is approximatily given by
U(x)=ax12−b)x6 where a and b are constant and x is the distance between the aloms , if the discision energy of the molecale is D=[U(x=∞)−U atequlibrium ] , D isAb22aBb212aCb24aDb26aThe potential energy between two atoms in a molecule is given by
U=ax2−bx2
where a and b are positive constants and x is the distance between the atoms. The atom is in stable equilibrium when x is equal to :−A0B2b3aC3a2bD3b2a
The potential energy function for the force between two atoms in a diatomic molecule is approximately given by U(x)=ax12−bx6 where a and b are constant and x is the distance between the atoms. Find the dissoociation energy of the molecule which is given as D=[U(x−∞)−Uatequilibrium]
View SolutionThe potential energy function for the force between two atoms in a diatomic molecule is approximate given by U(r)=ar12−br6, where a and b are constants and r is the distance between the atoms. If the dissociation energy of the molecule is D=[U(r=∞)−Uat equilibrium],D is
View SolutionThe potential energy between two atoms in a molecule is given by, U(x)=ax12−bx6 , where a and b are positive constant and x is the distance between the atoms. The atoms is an stable equilibrium, when-
View SolutionIf potential energy function for the force between two atoms in a diatomic molecule is approximately given by U(x)=ax8−bx4, where a and b are constants in standard SI units and x in meters. Find the dissociation energy of the molecule (in J). [Take a =4 J m8andb=20 J m4]
View SolutionIn a molecule, the potential energy between two atoms is given by U(x)=1x12−bx6. Where 'a' and 'b' are positive constants and 'x' is the distance between atoms. Find the value of 'x' at which force is zero and minimim P.E at that point.
View Solution
