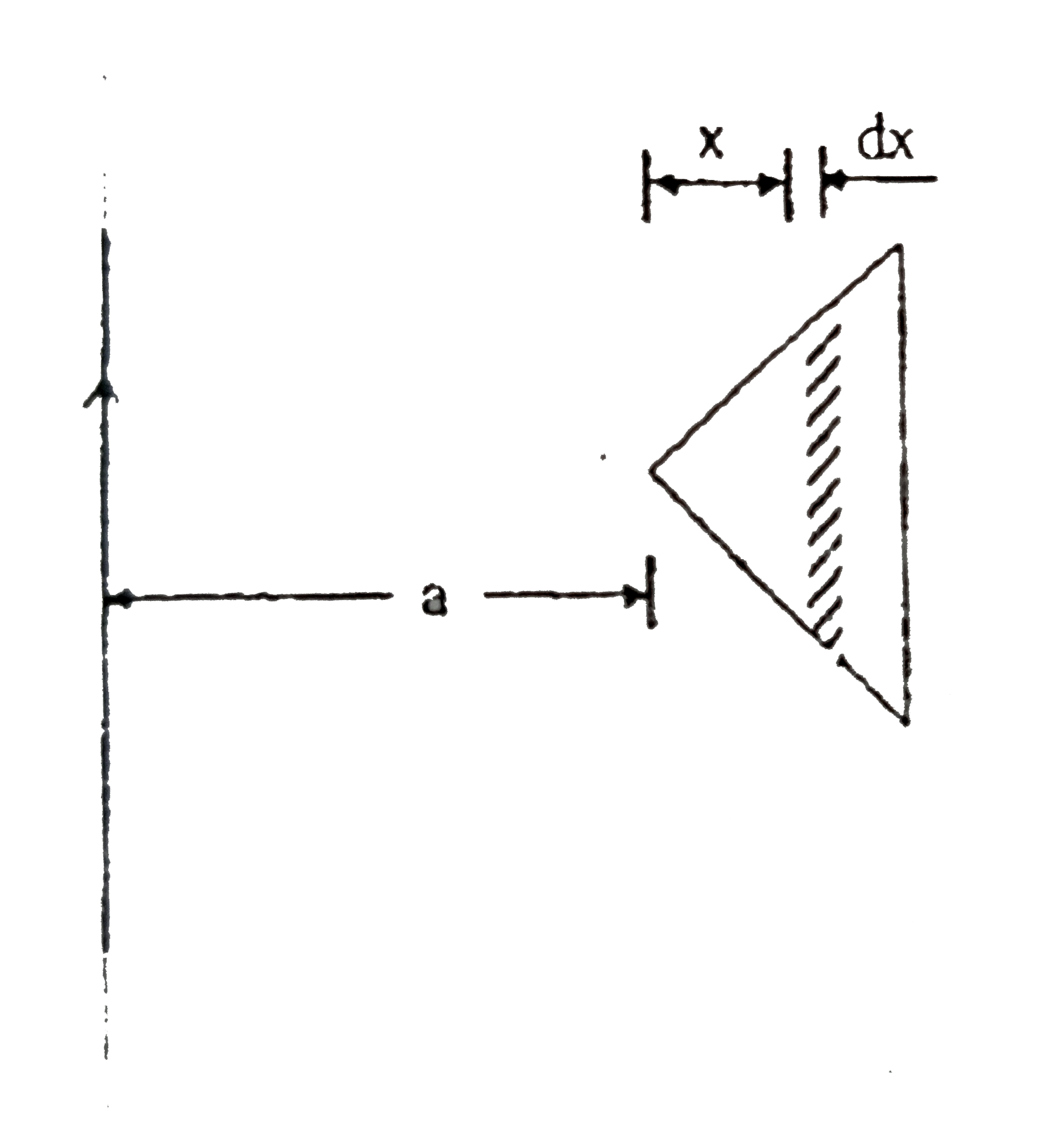
A very long staright conductor and an isoceles triangular conductor lie in a plane and separated from each other as shown in the figure.
Given a=10cm, b=20cm and h=10cm
(a) Find their coefficeint of mutual induction.
(b) If current in the staright wire is increasing at a rate of 2A/s , find the direction and magnitude of current in the triangular wire. [Diameter of the wire crosss-section d=1mm, resistivity of the wire, ρ=1.8×10−8Ω−m]
![A very long staright conductor and an isoceles triangular conductor lie in a plane and separated from each other as shown in the figure. Given a=10cm, b=20cm and h=10cm (a) Find their coefficeint of mutual induction. (b) If current in the staright wire is increasing at a rate of 2A//s , find the direction and magnitude of current in the triangular wire. [Diameter of the wire crosss-section d=1 mm, resistivity of the wire, rho=1.8xx10^(-8)Omega-m]](https://d10lpgp6xz60nq.cloudfront.net/physics_images/FIT_JEE_PHY_GMP_MOD3_C14_S01_044_Q01.png)
(a) Assuming a small strip at a distance x from the apex.
dA=bhxdx
Let I be the current folowing in the straight wire, then magnetic field at the location of the strip is
B=μ0I2π(a+x)
dϕ=BdA=μ0Ib2πh(xdxa+x)
ϕ=μ0Ib2πh∫h0[1−aa+x]dx
ϕ=μ0Ib2πh=[h−aln∣∣∣a+ha∣∣∣]
The coefficent of mutual induction is given by
M=ϕI=μ0b2πh[h−aln∣∣∣a+ha∣∣∣]
Here, b=20cm, h=10cm, μ0=4π×10−7H/m
M=(4π×10−7)(0.2)2π(0.1)[0.1−0.1ln∣∣∣10+1010∣∣∣]=1.22×10−8H
(b) According to Faraday's law
Eind=−Mdidt since, didt=2A/s
∴(Eind=(1.22×10−8)(2)=2.44×10−8 volt.
Resistance of the triangular conductor is R=ρ1A
here, rhp=1.8×10−8Ω−m, 1=10√2+20+10√2=20(√2+1)cm=0.48cm
A=π4(10−3)2=10−6π4m2
∴R=(1.8×10−8)(0.48)(3.14)×410−6=1.1×10−2Ω
I=EindR=2.44×10−81.1×10−2=2.2μA
The direction of the current is anticlockwise by Lenz Law.
Topper's Solved these Questions
Similar Questions
A very long straight conductor and an isosceles triangular conductor lie in a plane and are separated from each other as shown in the figure. If a = 10 cm, b = 20 cm, and h = 10 cm find the coefficient of mutual induction.
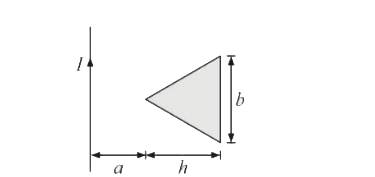
View SolutionA very long straight conductor and an isosceles triangular conductor lie in a plane and are separated from each other as shown in the figure. If a = 10 cm, b = 20 cm, and h = 10 cm find the coefficient of mutual induction.

View Solution
Knowledge Check
If a long straight wire carries a current of 40 A, then the magnitude of the field B at a point 15 cm away from the wire is
A5.34×10−5TB8.34×10−5TC9.6×10−5TD10.2×10−5TIf a long straight wire carries a current of 40 A, then the magnitude of the field B at a point 15 cm away from the wire is
A5.34×10−5TB8.34×10−5TC9.6×10−5TD10.2×10−5T
A very long straight conductor and an isosceles triangular conductor lie in a plane and are separated from each other as shown in the figure. If a = 10 cm, b = 20 cm, and h = 10 cm find the coefficient of mutual induction.

View SolutionA very long conductor and an isosceles triangular conductor lie in a plane and are separated from each other as shown in the figure. Find the coefficient of mutual induction. (a = 10 cm, b = 20 cm, h = 10 cm)
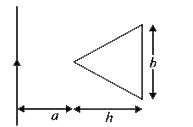
View SolutionA very long conductor and an isosceles triangular conductor lie in a plane and are separated from each other as shown in the figure. Find the coefficient of mutual induction. (a = 10 cm, b = 20 cm, h = 10 cm)

View SolutionA current carrying wire (straight) passes inside a triangular coil as shown in figure. The current in the wire is perpendicular to paper inwards. Find the direction of induced current in the loop if current in the wire is increasing with time.
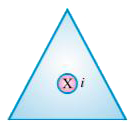
View SolutionA current carrying straight wire passes inside a triangular coil as shown in figure. The current in the wire is perpendicular to paper inwards. Find the direction of the induced current in the loop, if current in the wire is increased.
View SolutionA long straight wire carries a current of 35A. What is the magnitude of the field →B at a point 20cm from the wire?
View Solution
