A gas hydrogen like atoms can absorb radiations of $68 e V$ . Consequently, the atoms emit radiations of only three different wavelengths. All the wavelengths are equal or smaller than that of the absorbed photon.
( $a$ ) Determine the initial state of the gas atoms.
( $b$ ) Identify the gas atoms.
( $c$ ) Find the minimum wavelength of the emitted radiation.
( $d$ ) Find the ionization energy and the respective wavelength for the gas atoms.

Video Solution

Text Solution

Verified by Experts

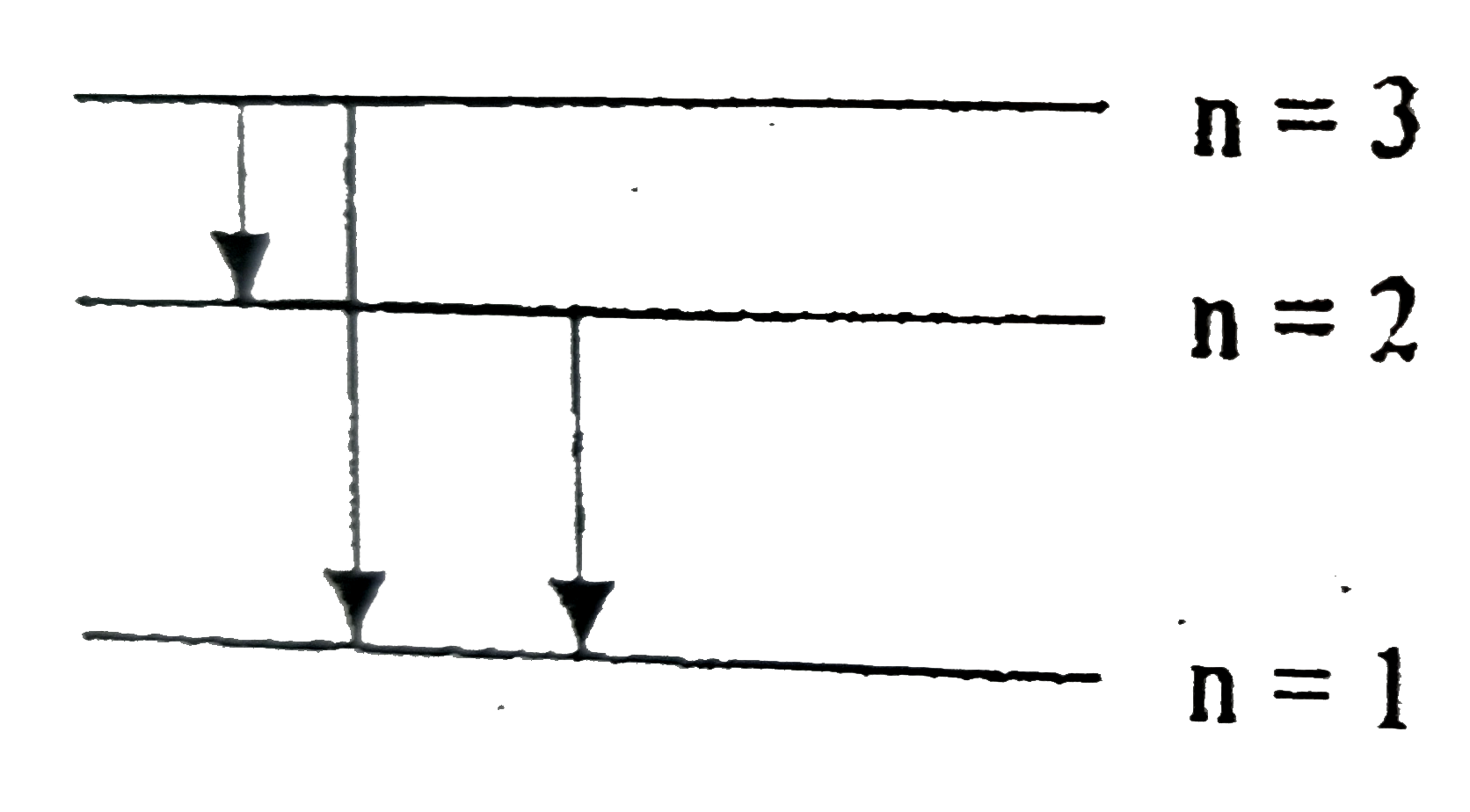
( $a$ ) Since three radiations are emitted, therefore, the final excited state of the gas is $n = 3$ .
The initial state of the gas atoms is
$n = 2$ as all the wavelengths are smaller and the energy will be higher.
( $b$ ) $13.6 Z^{2} [\frac{1}{2^{2}} - \frac{1}{3^{2}}] = 68$
or $13.6 Z^{2} [\frac{5}{36}] = 68 \Rightarrow Z = 6$
( $c$ ) The minimum wavelength corresponds to the transition $n = 3$ to $n = 1$ .
$\frac{1}{λ_{min}} = R Z^{2} [\frac{1}{1^{2}} - \frac{1}{3^{2}}]$
or $λ_{min} = \frac{9}{8 R Z^{2}} = \frac{9}{8 (1.097 \times 10^{7}) {(6)}^{2}} = 28.5 Å$
( $d$ ) The ionization energy of the gas atoms is
$E = 13.6 Z^{2} = (13.6) {(6)}^{2} = 489.6 e V$
$λ = \frac{1}{R Z^{2}} = \frac{1}{(1.097 \times 10^{7}) {(6)}^{2}} = 25.32 Å$

Hydrogen atom absorbs radiations of wavelength $λ_{0}$ and consequently emit radiations of 6 different wavelengths, of which two wavelengths are longer than $λ_{0}$ . Chosses the correct alternative(s).
AThe final excited staate of the atoms is n=4
BThe initial state of the atoms is n =2
CThe initial state of the atoms is n =3
DThere ae three transitions belonging to Lyman series
Find the wavelength of the emitted radiation,if electron in hydrogen atom jumps from third orbit to second orbit.
A $λ = \frac{36}{5 R}$
B $λ = \frac{5 R}{36}$
C $λ = \frac{5}{R}$
D $λ = \frac{R}{6}$
Which one among the following transitions of electron of hydrogen atom emits radiation of the shortest wavelength ?
An=2 to n=1
Bn=3 to n=2
Cn=4 to n=3
Dn=5 to n=4