Statement I: x2−5x+6<0 if 2<x<3 Statement II: If α and β,(α<β) are the roots of the equation ax2+bx+c=0 and α<x<β then ax2+bx+c and a have opposite signs
Step by step video & image solution for Statement I: x^2-5x+6<0 if 2 < x < 3 Statement II: If alpha and beta, (alpha < beta) are the roots of the equation ax^2+bx+c=0 and alpha < x < beta then ax^2+bx+c and a have opposite signs by Maths experts to help you in doubts & scoring excellent marks in Class 12 exams.
Updated on:21/07/2023Similar Questions
Statemenr I : If 3x+25=4x−76thenx=2312 Statement II: If 52x−938=2x then x = 69/5
View SolutionWrite the negation of following compound statements :
x = 2 and x = 3 are roots of the quadratic equation x2−5x+6=0
View Solution6x2+5x−6
View Solutionx=2 is a roots of the equation x2−5x+6=0. Is the given statement true?
View SolutionFor what value of x∈R the following expressions are negative
i) x2−5x−6 ii) −7x2+8x−9
View SolutionFor what values of x∈R, the following expressions are positive
i) x2−5x+6
View SolutionLet f(x)=x2−6x+5x2−5x+6. Then match the expressions/statements in List I with expression /statements in List II.

View SolutionLet f(x)=x2−6x+5x2−5x+6. Then match the expressions/statements in List I with expression /statements in List II.

View SolutionLet f(x)=x2−6x+5x2−5x+6 Match the expressions/ statements in Column I with expressions / Statement in column II.
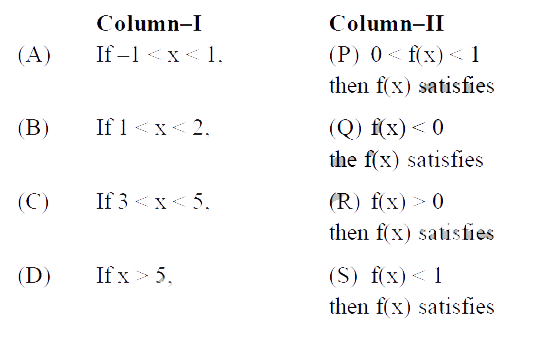
View SolutionDetermine whether the value given against each of the qaudratic equation are the roots of the equation.
(i) x2+5x−6=0,x=−6,2.
View Solution
