Let be a real valued continuous function on defined as The value of for which the curve intersect the curve at exactly two points, is (b) (c) (d)
A
B
C
D
Video Solution
Text Solution
The correct Answer is:A, D
Graph of 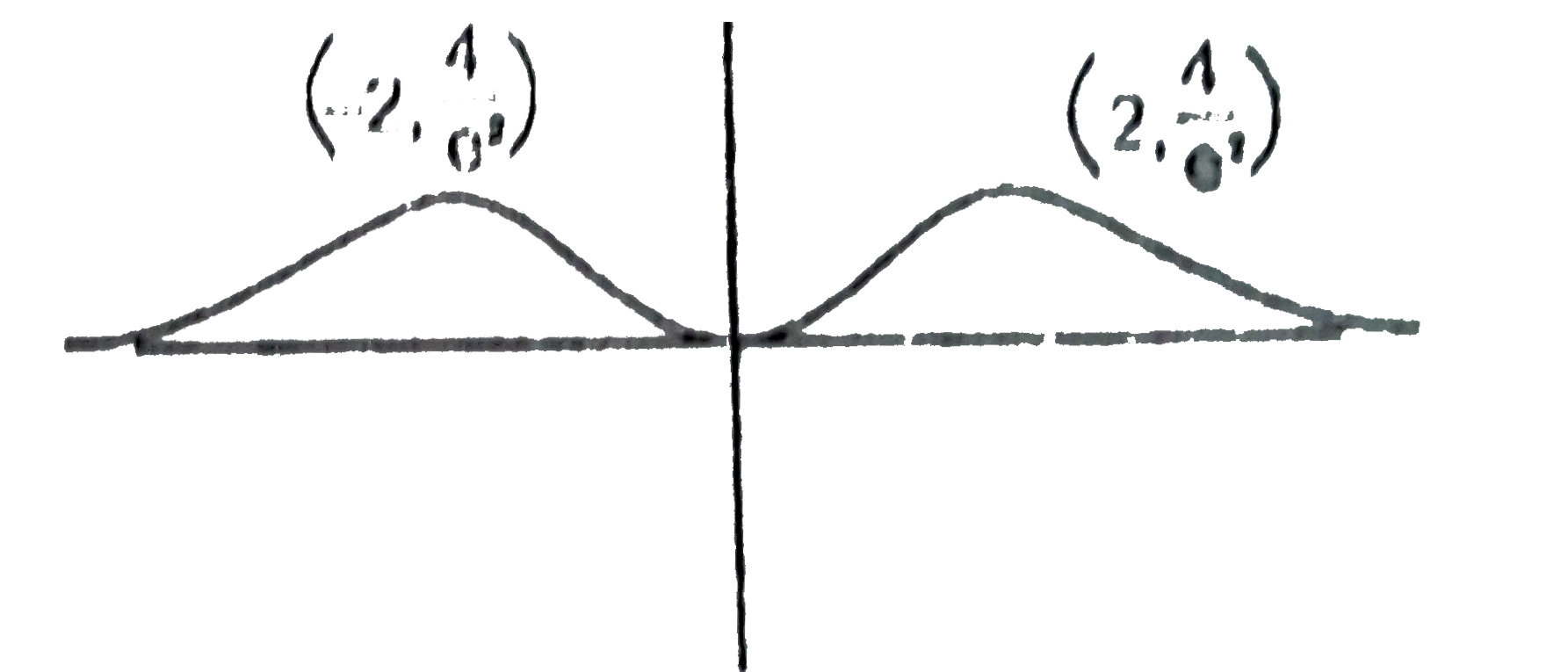
will intersect
Then
|
Topper's Solved these Questions
Similar Questions
Knowledge Check
Let f(x) be real valued continuous function on R defined as f(x)=x2e−|x| then f(x) is increasing in
A(0,2)B(2,∞)C(−2,0)D(−∞,2)Let f(X) be real valued continous funcion on R defined as f(X) =x2e−|x|
The values of k for which the equation x2e−|x|=k has four real roots areA0<k<eB0<k<8e2C0<k<4e2Dnone of theseLet f be a real valued function defined by f(x)=ex−e−|x|ex+e|x| , then the range of f(x) is: R (b) [0,1] (c) [0,1) (d) [0,12)
ARB[0,1]C[0,1)D[0,1/2)
Let f be a real valued function defined by f(x)=ex−e−|x|ex+e|x| , then the range of f(x) is: (a)R (b) [0,1] (c) [0,1) (d) [0,12)
View SolutionIf the curves y=2 ex and y=ae−x intersect orthogonally, then a= 1/2 (b) −1/2 (c) 2 (d) 2e2
View SolutionThe function f:R+→(1,e) defined by f(x)=x2+ex2+1 is
View SolutionLet the function f(x) be defined as f(x)={logx−1x−ex≠ekx=e
The value of k , for which the function is continuous at x =e , is equal to
View SolutionLet f:R→R be a function defined by f(x)=e|x|−e−xex+e−x, then f(x) is
View Solution
