There are two concentric and coplanar non-conducting rings of radii R and 4R. The charge is distributed uniormly on both rings. The charge on smaller ring is q and charge on large ring is −8q. A particle of mass 10g and charge −q is projected along the axis from infinity. What is the minimum speed of charge at infinity to reach the common centre of rings (take Kq2R=2√53J)
5m/s
10m/s
20m/s
30m/s
The correct Answer is:C
→Eq+→E8q=→0
⇒Kqx(R2+x2)3/2=k(8q)x(16R2+x2)(3/2)
⇒x=2R
In region x>2R electrostatics force is repulsive
in region 0<x<2R electrostatics force is attractive
If change paticle crosses x=2R it will reach origin so by conservation of energy
∴12mv2=−kq×q√R2+x2+k(8q)×q√16R2+x2
⇒v=20m/s
Topper's Solved these Questions
Similar Questions
Knowledge Check
A thin conducting ring of radius R is given a charge +Q. The electric field at the centre O of the ring due to the charge on the part ABCD of the ring is
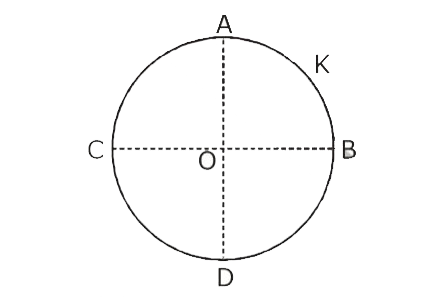 A3E along KOBE along OKCE along KOD3 E along OK
A3E along KOBE along OKCE along KOD3 E along OKA conducting ring of radius R has charge Q distributed unevenly over it. If it rotates with an angular velocity ω, the equivalent current will be
AzeroBQωCQω2πDQω2πRA point charge q of mass m is located at the centre of a ring having radius R and charge Q. When it is displaced slightly, the point charge accelerates along the x-axis to infinity, the ultimate speed of the point charge :-
A√2kQqmRB√kQqmRC√kQq2mRDzero
A non-conducting ring of radius R has charge Q distributed unevenly over it. If it rotates with an angular velocity ω the equivalent current will be:

View SolutionTwo concentric rings placed in a gravity free region in yz-plane one of radius R carries a+Q and second of radius 4R and charge –8Q distributed uniformly over it. Find the velocity with which a point charge of mass m and charge +q should be projected from a a distance 3R from the centre of rings on its axis so that it will reach to the centre of the rings.
View SolutionOver a thin ring of radius R a charge q is distributed none-uniformly. Calculate the work done of the force field in displacing a point charge q' from centre of the ring to infinity.
View SolutionA charge Q is distributed uniformly on a ring of radius R as shown in the following diagrams. Find the electric potential at the centre O of the ring

View SolutionCharges q is uniformly distributed over a thin half ring of radius R. The electric field at the centre of the ring is
View Solution

