If the focus of a parabola is (3,3) and its directrix is 3x−4y=2 then the length of its latus rectum is
2
4
3
5
The correct Answer is:A
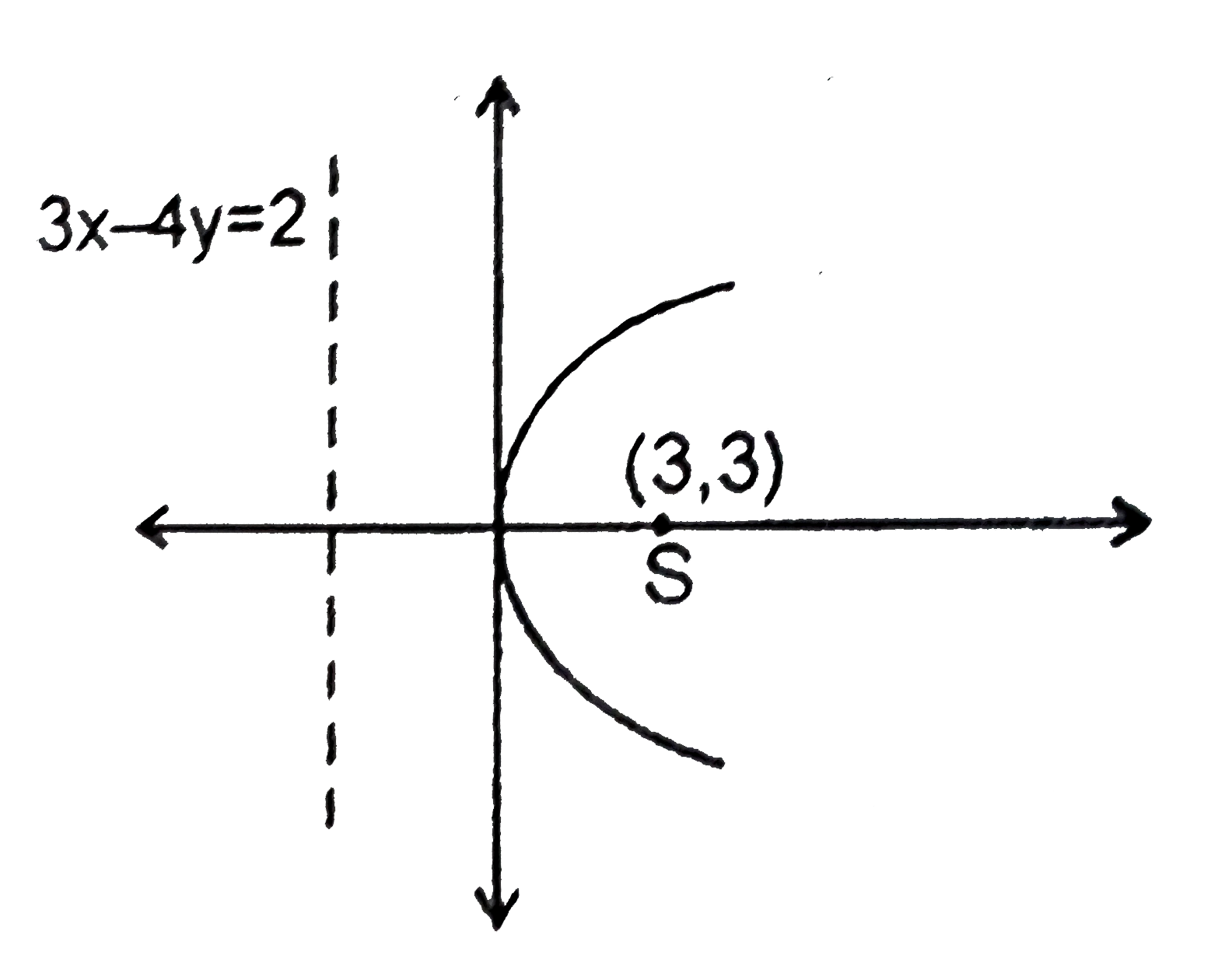
2A=∣∣
∣∣3(3)−4(3)−2√32+42∣∣
∣∣⇒2A=55=1
L.R. =4A=2
Topper's Solved these Questions
Similar Questions
The vertex of a parabola is at (4,3) and directrix is x−y+1=0. Then the equation of its latus rectum is
View SolutionFind the coordinates of the point of intersection of the axis and the directrix of the parabola whose focus is (3,3) and directrix is 3x−4y=2. Find also the length of the latus rectum.
View Solution
Knowledge Check
If the focus of a parabola is (0,−3) and its directrix is y=3, then its equation is
Ax2=−12yBx2=12yCy2=−12xDy2=12xIf the focus of a parabola is at (0,-3) and its directrix is y = 3, then its equation is
Ax2=−12yBx2=12yCy2=−12xDy2=112xIf the focus of parabola is at (0,-2) and its directrix is y=3, then its equation is
Ax2=−12yBx2=12yCy2=−12yDy2=12x
Focus of a parabola is (2,3) and directrix is x−4y+t=0 and its length of latus rectum is 14√17 ,then t is equal to (t is a single digit integer)
View SolutionVertex is (4,3) and directrix is 3x+2y−7=0 then equation to latus rectum is
View SolutionFind the co-ordinates of the focus, axis of the parabola, the equation of the directrix and the length of the latus rectum
y2=−18x.
View SolutionIf the focus of a parabola is (2, 3) and its latus rectum is 8, then find the locus of the vertex of the parabola.
View SolutionIf the focus of a parabola is at (0, -3) and its directrix is y = 3, then its equation is
View Solution
