A circular loop is bent so that half of (OAB) lies in xy- plane ane the other half (OCB) lie in xz-plane. A time varying magnetic field axis here given by B=α(tˆj−2tˆk) where α is a positive constant. What will be the direction of induced current.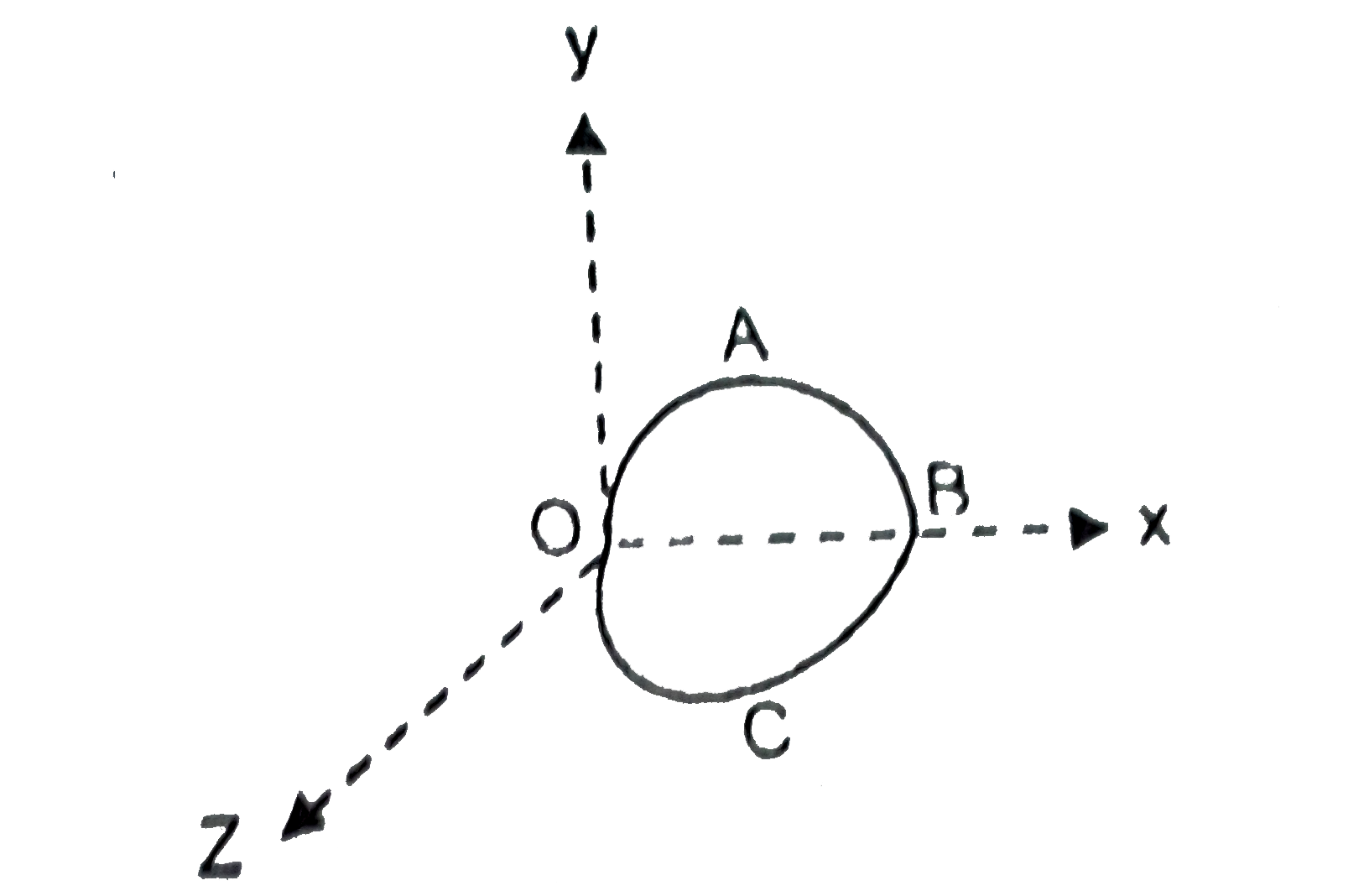 
OCBAO
OABCO
BAO in one part and BCO in the other part
induced current will be zero
NA
Topper's Solved these Questions
Similar Questions
A rectangular wire loop with length a and width b lies in the xy-plane as shown. Within the loop, there is a time dependent magnetic field given by →B=c[(xcosωt)ˆi+(ysinωt)ˆk]. Here , c and ω are constants. The magnitude of emf induced in the loop as function of time is
View SolutionA rectangular loop of wire oriented with the left corner at the origin one edge along X -axis and the other along Y axis as shown in the A magnetic field is into the page and has a magnitude that is given by b=αy where α is contant Find the total magnetic force on the loop if it carries current
View Solution
Knowledge Check
- Question 1 - Select One
A non-planar circular loop consists of two semi-circles one of which lies in yz-plane & the other is in xz-plane as shown.The magnetic force experienced by positive charge of value Q moving with velocity v along x direction when it is at the origin is:
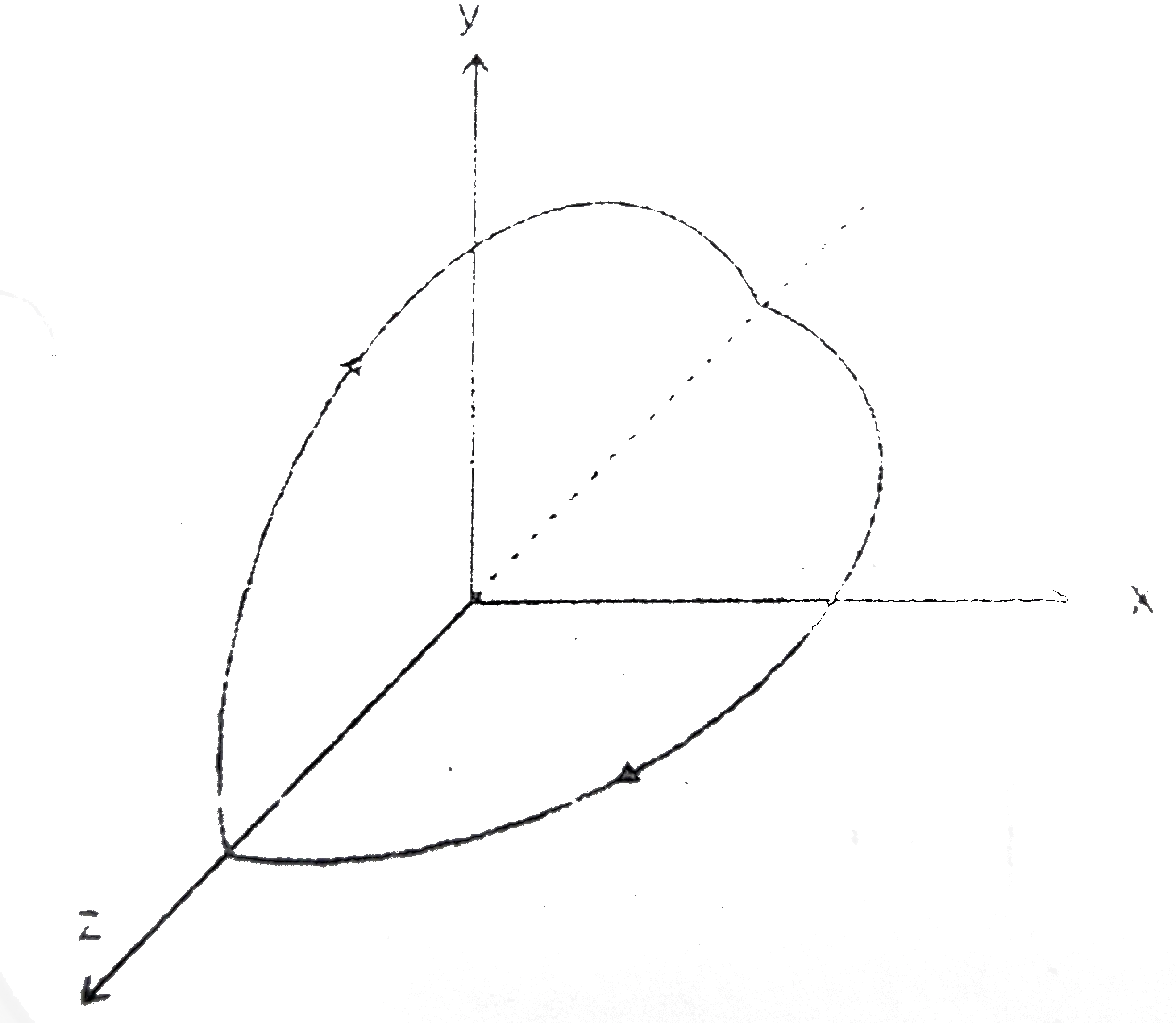AQvμ0I4RBQvμ0I2RCQvμ0I2√2RD0 - Question 2 - Select One
A rectangular loop of sides of length l and b is placed in x-y plane. A uniform but time varying magnetic field of strength →B=20tˆi+10t2ˆj+50ˆk where t is time elapsed. The magnitude of induced emf at time t is:
A20+20tB20C20tDzero - Question 3 - Select One
In Fig ABCDEFA was a square loop of side l, but is folded in two equal parts so that half of it lies in the x-z plane and the other half lies in the y-z plane. The origin O is centre of the frame also. The loop carries current 'i'. The magnetic field at the centre is
Aμ0i2√2πl(ˆi−ˆj)Bμ0i4πl(−ˆi−ˆj)C√2μ0iπl(ˆi+ˆj)Dμ0i√2πl(ˆi+ˆj)
A square loop ABCD of side l is moving the xy plane with velocity →v=βtˆj.There exists a non-uniform magnetic field →B=−B0(1+αy2)ˆk(y>0), where B0 and α are positive constants. Initially, the upper wire of the loop is at y=0.Find the induced voltage across the resistance R as a function of time.Neglect the magnetic force due to induced current.
View SolutionA wire is bent in the form of a square of side 'a' in a varying magnetic field ¯¯¯B=αB0tˆk. If the resistance per unit length is λ, then find the following.
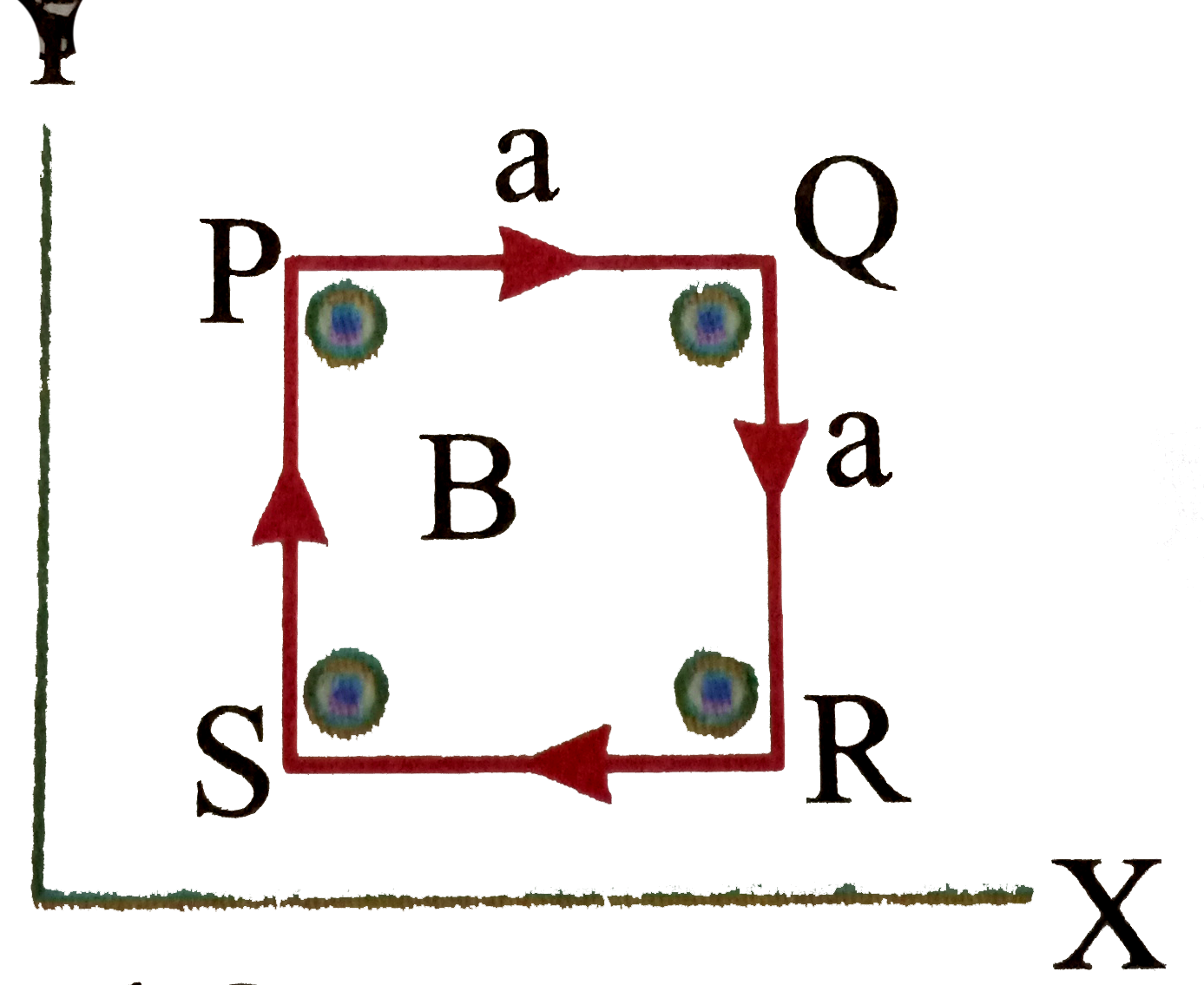
i) The direction of induction current
ii) The current in the loop
iii) Potential difference between P and QView SolutionA circular loop of radius R carrying current I is kept in XZ plane. A uniform and constant magnetic field →B=(B0ˆi+2B0ˆj+3B0ˆk) exists in the region (B0− a positive constant). Then the magnitude of the torque acting on the loop will be
View SolutionA rectangular loop of wire is oriented with the left corner at the origin, one edge along X-axis and the other edge along Y-axis as shown in the figure. A magnetic field is into the page and has a magnitude that is given by β=αy
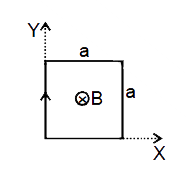
where α is constant. Find the total magnetic force on the loop if it carries carrent i.View SolutionA circular loop carrying a current I is placed in the xy-plane as shown in figure. A uniform magnetic fied B is oriented along the positive z-axis. The loop tends to
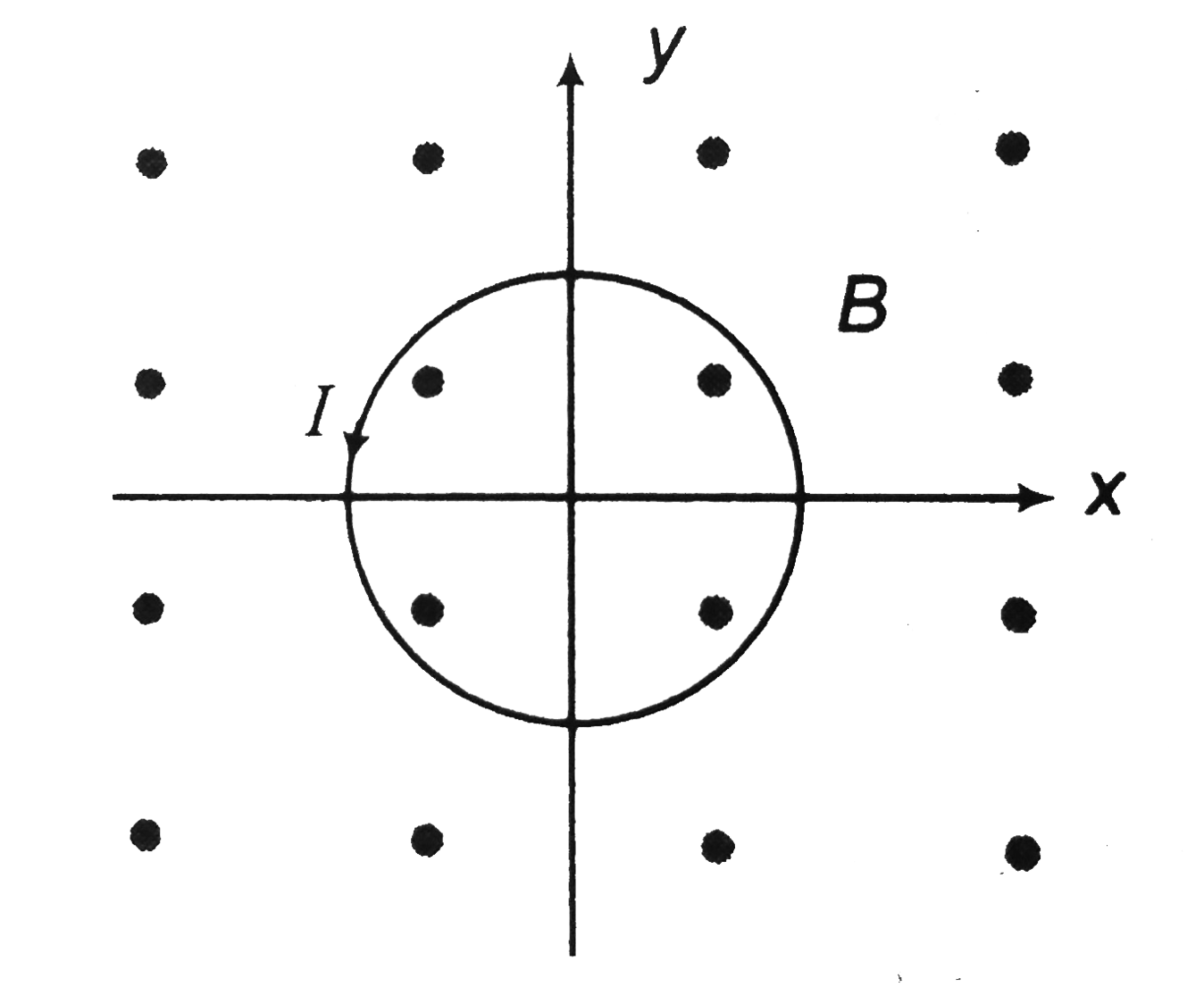
View Solution